Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Ерөнхий шүргэгч
$y=x^2+4x+8$ параболын $x=x_1$ абсцисстай цэгт татсан шүргэгч шулууны тэгшитгэл нь $$y=(2x_1+\fbox{a})x+\fbox{b}-x_1^2,$$ $y=x^2+8x+4$ параболын $x=x_2$ абсцисстай цэгт татсан шүргэгч шулууны тэгшитгэл нь $$y=(2x_2+\fbox{c})x+\fbox{d}-x_2^2$$ байна. Иймд параболуудын ерөнхий шүргэгч нь $$y=\fbox{e}x+\fbox{f}$$ байна.
ab = 48
cd = 84
ef = 84
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 44.74%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $y=f(x)$ функцийн графикийн $(x_0,f(x_0))$ цэгт татсан шүргэгч шулууны тэгшитгэл
$$y=f^\prime(x_0)(x-x_0)+f(x_0)$$
байна.
$y=ax^2+bx+c$ функцийн уламжлал нь $y^\prime=2ax+b$ байна.
$y=ax^2+bx+c$ функцийн уламжлал нь $y^\prime=2ax+b$ байна.
Бодолт: $(x^2+4x+8)^\prime=2x+4$ тул $y=x^2+4x+8$ параболын $x=x_1$ абсцисстай цэгт татсан шүргэгч шулууны тэгшитгэл нь
$$y=(2x_1+4)(x-x_1)+x_1^2+4x_1+8=(2x_1+4)x+8-x_1^2$$
$(x^2+8x+4)^\prime=2x+8$ тул $y=x^2+8x+4$ параболын $x=x_2$ абсцисстай цэгт татсан шүргэгч шулууны тэгшитгэл нь
$$y=(2x_2+8)(x-x_2)+x_2^2+8x_2+4=(2x_2+8)x+4-x_2^2$$
байна.
Эдгээр нь нэг шулуун байхын тулд $\left\{\begin{array}{c}2x_1+4=2x_2+8\\8-x_1^2=4-x_2^2\end{array}\right.$ байна. Эхний тэгшитгэлээс $x_2=x_1-2$ болох ба үүнийг 2-д орлуулбал $$8-x_1^2=4-(x_1-2)^2\Leftrightarrow 8-x_1^2=4-x_1^2+4x_1-4$$ буюу $x_1=2$ байна. Иймд ерөнхий шүргэгчийн тэгшитгэл нь $$y=(2\cdot 2+4)x+8-2^2=8x+4$$ байна.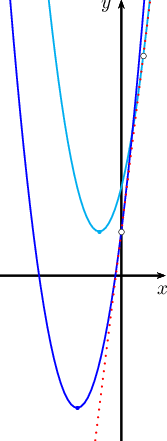
Эдгээр нь нэг шулуун байхын тулд $\left\{\begin{array}{c}2x_1+4=2x_2+8\\8-x_1^2=4-x_2^2\end{array}\right.$ байна. Эхний тэгшитгэлээс $x_2=x_1-2$ болох ба үүнийг 2-д орлуулбал $$8-x_1^2=4-(x_1-2)^2\Leftrightarrow 8-x_1^2=4-x_1^2+4x_1-4$$ буюу $x_1=2$ байна. Иймд ерөнхий шүргэгчийн тэгшитгэл нь $$y=(2\cdot 2+4)x+8-2^2=8x+4$$ байна.