Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Квадратыг багтаасан ба квадратад багтсан тойрог
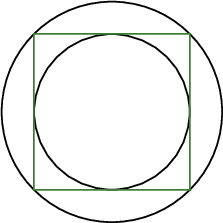
Квадратыг багтаасаан тойргийн уртыг, уг квадратад багтсан тойргийн уртад харьцуулсан харьцааг ол.
A.$2$ B.$\sqrt2$ C.$\dfrac{1}{\sqrt2}$ D.$2\sqrt2$ E.$\dfrac12$
Бодлогын төрөл:Сонгох
Амжилтын хувь:43.53%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:Квадратын диагоналын уртаар тойргуудын радиусуудыг илэрхийл.
Бодолт:$d$ диагоналын урт бол багтаасан тойргийн радиус нь $R=\dfrac{d}{2}$, багтсан тойргийн радиус нь квадратын талын уртын хагас буюу $r=\dfrac{d}{2\sqrt2}$ байна. Иймд уртуудын харьцаа нь
$$\dfrac{\ell_1}{\ell_2}=\dfrac{2\pi R}{2\pi r}=\dfrac{R}{r}=\dfrac{\frac{d}{2}}{\frac{d}{2\sqrt2}}=\sqrt2$$
байна.
Сорилго
2017-09-23 hw-56-2016-06-15 Хавтгайн геометр 2 Сорилго 2 А хувилбар Сорилго 2 Б хувилбар Сорилго 2 Б хувилбар сорил-5 Дунд сургуулийн геометр 99 99 тестийн хуулбар Тойрог, түүнтэй холбоотой бодлогууд багтсан ба багтаасан 4 өнцөгт багтсан ба багтаасан 4 өнцөгт тойрог ба олон өнцөгт Хавтгайн геометр 2 тестийн хуулбар 2021-05-10 сорил 2021-05-10 сорил Геометр /хавтгай/ Багтсан ба багтаасан тойрог