Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Координатын хавтгайд цэгүүдийг дүрслэх
$A(5,4)$, $B(2,2)$, $C(-4,6)$ бол $ABC$ гурвалжны $AM$ медианы уртыг ол.
A.2 B.5 C.6 D.8 E.10
Бодлогын төрөл:Сонгох
Амжилтын хувь:77.16%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:Координатын хавтгай дээр зураад хар.
$M_1(x_1;y_1)$, $M_2(x_2;y_2)$ бол $M_1M_2$ хэрчмийн дундаж цэгийн координат нь $$\color{red}{\left(\dfrac{x_1+x_2}{2};\dfrac{y_1+y_2}{2}\right)}$$ ба хоорондох зай нь $$\color{red}{M_1M_2=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}$$ байна.
$M_1(x_1;y_1)$, $M_2(x_2;y_2)$ бол $M_1M_2$ хэрчмийн дундаж цэгийн координат нь $$\color{red}{\left(\dfrac{x_1+x_2}{2};\dfrac{y_1+y_2}{2}\right)}$$ ба хоорондох зай нь $$\color{red}{M_1M_2=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}$$ байна.
Бодолт: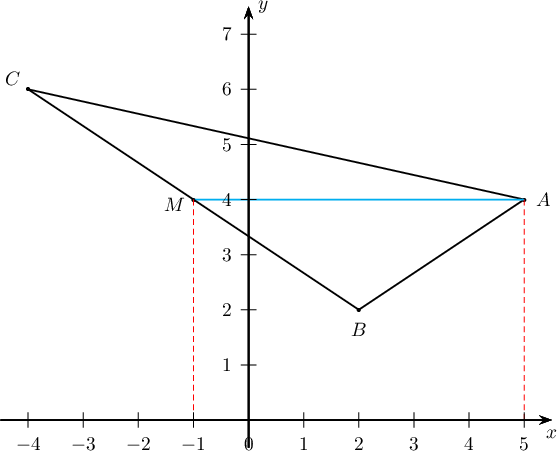
Зургаас харахад $BC$ хэрчмийн дундаж цэг нь $$M=\dfrac{B+C}{2}=M\left(\dfrac{2+(-4)}{2};\dfrac{2+6}{2}\right)=M(-1;4)$$ байна. $AM$ нь $OX$ тэнхлэгтэй параллель тул $AM=|5-(-1)|=6$ байна.
Сорилго
2017-09-27 4.29 Координатын арга. Хавтгайн координатын арга. координатын геометр 2 цэгийн хоорондох зай Хувиргалт