Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Биссектрисийн урт
$\triangle ABC$-ийн $AB=4$, $AC=6$ ба $\measuredangle BAC=60^\circ$ байв. $A$ оройгоос татсан биссектрисийн уртыг ол.
A.$\dfrac{12\sqrt3}{5}$ B.$3\sqrt{3}$ C.$4\sqrt3$ D.$\dfrac{4\sqrt3}{3}$ E.$2\sqrt{3}$
Бодлогын төрөл:Сонгох
Амжилтын хувь:55.22%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
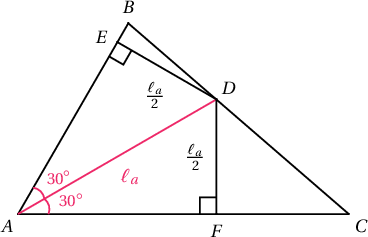
Заавар:Биссектрисээр хуваагдсан хоёр гурвалжны биссектрисийн сууриас татсан өндрүүд хоорондоо тэнцүү $\ell_a\sin30^\circ$ болохыг ашиглан гурвалжны талбайг олж бод.
Шууд косинусын теорем ашиглан гурав дахь талын уртыг олоод биссектрисийн уртыг олох $$\ell_a=\sqrt{bc-\dfrac{a^2bc}{(b+c)^2}}$$ томьёо ашиглан бодож болно.
Шууд косинусын теорем ашиглан гурав дахь талын уртыг олоод биссектрисийн уртыг олох $$\ell_a=\sqrt{bc-\dfrac{a^2bc}{(b+c)^2}}$$ томьёо ашиглан бодож болно.
Бодолт:$S_{\triangle ADB}=\dfrac{4\cdot\frac{\ell_a}{2}}{2}=\ell_a$, $S_{\triangle ADC}=\dfrac{6\cdot\frac{\ell_a}{2}}{2}=1.5\ell_a$ ба
$$S_{\triangle ADB}+S_{\triangle ADC}=S$$ тул$$\ell_a+1.5\ell_a=\dfrac12\cdot 4\cdot 6\cdot\sin60^\circ$$
болно. Иймд $\ell_a=\dfrac{12\sqrt3}{5}$ байна.
Жич: Өнцгийн биссектрис нь тухайн өнцгийг үүсгэж буй цацрагуудаас ижил зайд алслагдсан цэгүүдийн олонлог байдаг.
Сорилго
2017-10-03 Даалгавар №1 2016-11-09 geometr Геометр сэдвийн давтлага 2 2020-03-10 сорил Косинусын теорем Косинусын теорем тестийн хуулбар 11-анги Ерөнхий давтлага Синус, косинусын теорем Геометр сэдвийн давтлага 2 тестийн хуулбар