Монгол Бодлогын Сан

Заавар: $$|a|< b\Leftrightarrow -b< a< b$$ ба $$|a|>b\Leftrightarrow a<-b\lor a>b$$ адилтгал хувиргалтуудыг ашиглан модультай илэрхийллийг боддог.

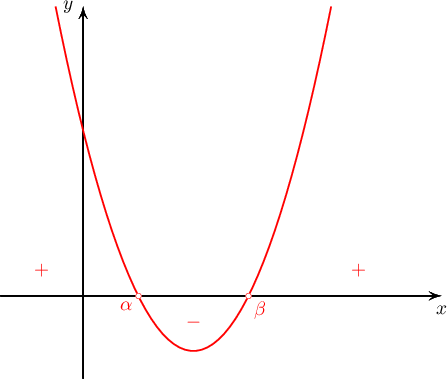
$a>0$ (дээшээ харсан парабол) ба $\alpha<\beta$ бол $$0< a(x-\alpha)(x-\beta)$$ тэнцэтгэл бишийн шийд нь $x<\alpha\lor x>\beta$, харин $$a(x-\alpha)(x-\beta)<0$$ тэнцэтгэл бишийн шийд нь $\alpha< x< \beta$ байна.

Бодолт: $$-3<2-\dfrac{1}{x-4}<3\Leftrightarrow -5<-\dfrac{1}{x-4}<1$$ болно. Давхар тэнцэтгэл биш нь систем тэнцэтгэл биш болох тул $$\left\{\begin{array}{c} -5<-\dfrac{1}{x-4}\\dfrac{1}{x-4}<1\end{array}\right.\Leftrightarrow\left\{\begin{array}{c} 0<-\dfrac{1}{x-4}+5^{\color{red}{(x-4}}\\0<1^{\color{red}{(x-4}}+\dfrac{1}{x-4}\end{array}\right.\Leftrightarrow$$ $$\left\{\begin{array}{c} 0<\dfrac{-1+5(x-4)}{x-4}\\0<\dfrac{(x-4)+1}{x-4}\end{array}\right.\Leftrightarrow\left\{\begin{array}{c} 0<\dfrac{5x-21}{x-4}\\0<\dfrac{x-3}{x-4}\end{array}\right.$$ болно. $\color{red}{\dfrac{a}{b}<0\Leftrightarrow ab<0}$ тул $$\left\{\begin{array}{c} 0<5(x-4)\big(x-\frac{21}{5}\big)\\0<(x-3)(x-4)\end{array}\right.$$ тэнцэтгэл бишийн систем болно. $\Big\{$ системийн шийд нь тэнцэтгэл бишүүдийн шийдүүдийн огтлолцол байна. Иймд $x\in]-\infty;3[\cup\Big]\dfrac{21}{5};+\infty\Big[$