Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Тэгш өнцөгт гурвалжин
Тэгш өнцөгт гурвалжны гипотенуз дээрх катетуудын проекц 25, 144 бол тэгш өнцгийн оройгоос татсан өндөр $\fbox{ab}$ болно. Богино катет нь $\fbox{cd}$, урт катет нь $\fbox{efg}$ болох бөгөөд уг гурвалжинд багтсан тойргийн радиус $r=\fbox{hi}$ байна.
ab =60
cd =65
efg =156
hi =26
Бодлогын төрөл:Нөхөх
Амжилтын хувь:58.99%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар: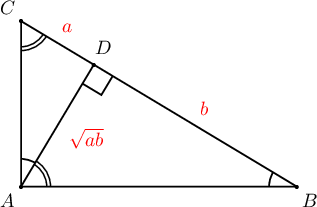
$\triangle ABC$ тэгш өнцөгт гурвалжинд $AD$ өндөр татвал $\triangle ADC\sim\triangle BDA$ тул $$\dfrac{CD}{AD}=\dfrac{AD}{BD}\Rightarrow AD=\sqrt{CD\cdot DB}=\sqrt{ab}$$
байна.
Багтсан тойргийн радиус нь $$r=\dfrac{AC+AB-BC}{2}$$ байна. Эсвэл $r=\dfrac{S}{p}=\dfrac{2S}{P}$ томьёогоор ч олж болно.
Багтсан тойргийн радиус нь $$r=\dfrac{AC+AB-BC}{2}$$ байна. Эсвэл $r=\dfrac{S}{p}=\dfrac{2S}{P}$ томьёогоор ч олж болно.
Бодолт:$a=25$, $b=144$ тул $h=\sqrt{25\cdot 144}=60$ байна. Эндээс Пифагорын теорем бичиж бага катетын уртыг олбол $\sqrt{25^2+60^2}=65$ байна. Нөгөө катетын урт нь $\sqrt{144^2+60^2}=156$ байна.
Багтсан тойргийн радиус нь $r=\dfrac{65+156-169}{2}=26$ байна.
Багтсан тойргийн радиус нь $r=\dfrac{65+156-169}{2}=26$ байна.