Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Трапецийн талбай
$AD\parallel BC$ байх трапецийн $AB=5$, $BC=8$, $BD=7$, $\angle A=120^\circ$ байв. Трапецийн талбайг ол.
A.$\dfrac{55\sqrt3}{4}$ B.$55$ C.$11\sqrt{3}$ D.$75$ E.$26$
Бодлогын төрөл:Сонгох
Амжилтын хувь:61.76%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:Трапецийн талбай нь сууриудын уртын нийлбэрийн хагасыг трапецийн өндрөөр үржүүлсэнтэй тэнцүү байдаг. Трапецийн өндрийг $h$ гэвэл
$$S=\dfrac{AD+BC}{2}\cdot h$$
байна.
Косинусын теорем ашиглан $AD$ талын уртыг ол.
$AH$ өндөр татан $\triangle AHB$ тэгш өнцөгт гурвалжнаас трапецийн өндрийг олоорой.
Косинусын теорем ашиглан $AD$ талын уртыг ол.
$AH$ өндөр татан $\triangle AHB$ тэгш өнцөгт гурвалжнаас трапецийн өндрийг олоорой.
Бодолт: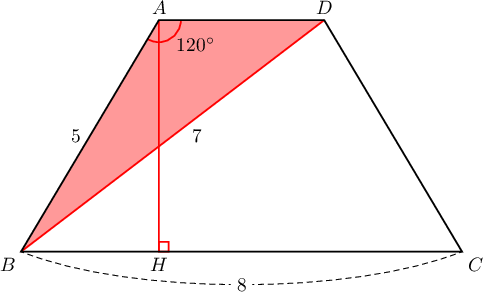
$\triangle ABD$-д косинусын теорем бичвэл
$$7^2=5^2+AD^2-2\cdot 5\cdot AD\cos120^\circ$$
буюу
$$AD^2+5AD-24=0\Leftrightarrow(AD-3)(AD+8)=0$$
болно. $AD>0$ тул $AD=3$ байна. Нөгөө талаас
$$h=AH=AB\sin\angle B=5\sin60^\circ=\dfrac{5\sqrt3}{2}$$
Иймд
$$S=\dfrac{AD+BC}{2}\cdot AH=\dfrac{3+8}{2}\cdot\dfrac{5\sqrt3}{2}=\dfrac{55\sqrt3}{4}$$
байна.
Сорилго
2017-10-08 Даалгавар №1 geometr 2020-03-10 сорил Дунд сургуулийн геометр Косинусын теорем Косинусын теорем тестийн хуулбар