Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Гурвалжныг бодох
$\triangle ABC$-ийн хувьд $a=2$, $b=\sqrt2$, $c=1$ байв.
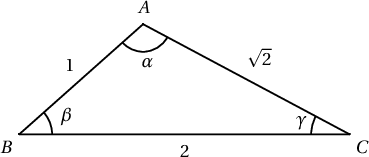
- $\cos\beta=\dfrac{\fbox{a}}{4}$, $\sin\beta=\dfrac{\sqrt{\fbox{b}}}{4}$;
- Гурвалжны талбай нь $S_{\triangle ABC}=\dfrac{\sqrt{\fbox{c}}}{\fbox{d}}$;
- Багтсан тойргийн радиус нь $r=\dfrac{\sqrt{7}(\fbox{e}-\sqrt{\fbox{f}})}{14}$;
- Багтаасан тойргийн радиус нь $R=\dfrac{\fbox{g}\sqrt{14}}{\fbox{h}}$ байна.
a = 3
b = 7
cd = 74
ef = 32
gh = 27
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 50.90%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар:
- Косинусын теорем ба тригонометрийн үндсэн адилтгал ашигла.
- $S=\dfrac12ca\sin\beta$ томьёог ашигла.
- $r=\dfrac{2S}{a+b+c}$ байна.
- Синусын теорем ашигла: $R=\dfrac{b}{2\sin\beta}$.
Бодолт:
- Косинусын теоремоор: $$\cos\beta=\dfrac{1^2+2^2-(\sqrt2)^2}{2\cdot1\cdot 2}=\dfrac{3}{4}$$ $\sin\beta>0$ тул үндсэн адилтгалаар $$\sin\beta=\sqrt{1-\Big(\dfrac34\Big)^2}=\dfrac{\sqrt{7}}{4}$$
- $S=\dfrac12ca\sin\beta=\dfrac12\cdot1\cdot 2\cdot\dfrac{\sqrt{7}}{4}=\dfrac{\sqrt{7}}{4}$ байна.
- $r=\dfrac{2S}{a+b+c}=\dfrac{\frac{\sqrt7}{2}}{2+\sqrt2+1}=\dfrac{\sqrt7}{2(3+\sqrt2)}=\dfrac{\sqrt{7}(3-\sqrt2)}{14}$
- $R=\dfrac{b}{2\sin\beta}=\dfrac{\sqrt2}{2\cdot\frac{\sqrt7}{4}}=\dfrac{2\sqrt2}{\sqrt7}=\dfrac{2\sqrt{14}}{7}$ байна.
Сорилго
2017-10-09
2016-05-23
hw-56-2016-06-15
2016-11-08
Косинусын теорем
Хавтгайн геометр 2
тригонометр илэрхийлэл
Косинусын теорем
Косинусын теорем тестийн хуулбар
2020-12-21 сорил
Синус, косинусын теорем
Хавтгайн геометр 2 тестийн хуулбар
Косинус ба синусын теорем