Монгол Бодлогын Сан

Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.

$f(x)=(\sqrt3\sin x+3\cos x)^2$ байг.

$f(x)=\fbox{a}\sin(2x+\fbox{bc}^\circ)+\fbox{d}$ болно.
$f(x)=1$ тэгшитгэлийн $0^\circ\le x<360^\circ$ байх шийдийн тоо $\fbox{e}$ ширхэг байна. Эдгээр шийдээс хамгийн их, багыг нь харгалзан $\alpha$, $\beta$ гэвэл $\alpha+\beta=\fbox{fgh}^\circ$ байна.

abcd = 6306

e = 4

fgh = 420

Бодлогын төрөл: Нөхөх

Амжилтын хувь: 40.34%

Заавар:

$\sin\alpha+\sqrt3\cos\alpha=2\sin(\alpha+60^\circ)$, $2\sin^2\alpha=1-\cos2\alpha$, $\cos\alpha=\sin(90^\circ-\alpha)$ томьёог ашигла.
Графикийг зурж хар.

Бодолт:

\begin{align*} (\sqrt3\sin x+3\cos x)^2&=(\sqrt3)^2(\sin x+\sqrt3\cos x)^2\\ &=12\sin^2(x+60^\circ)=6\cdot(1-\cos(2x+120^\circ))\\ &=6-6\cdot\sin (90^\circ-(2x+120^\circ))=6-6\sin(-2x-30^\circ) \end{align*} болно. Синус нь сондгой функц тул $$f(x)=6\sin(2x+30^\circ)+6$$ болно.
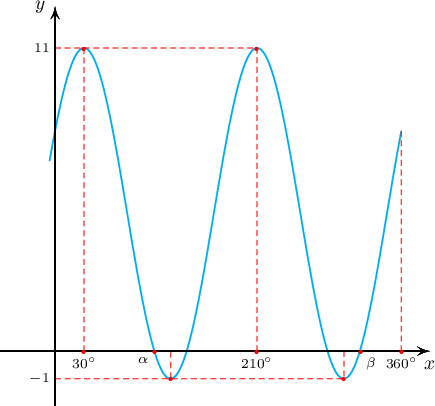
$y=f(x)-1=6\sin(2x+30^\circ)+5$ функцийн графикийг зуръя.
Зургаас харахад уг функцийн график $OX$ тэнхлэгийг 4 цэгээр огтлох бөгөөд тэдгээр нь $\gamma=210^\circ$ өнцгийн хувьд тэгш хэмтэй байрлаж байна. Иймд $f(x)=1$ тэгшитгэл $0\le x< 360^\circ$ байх 4 шийдтэй бөгөөд хамгийн их ба багынх нь нийлбэр $$\alpha+\beta=2\gamma=420^\circ$$ байна.