Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Шийдүүдийн бүхэл хэсгүүдийн нийлбэр
$x^3-3x^2+3=0$ тэгшитгэлийн шийдүүдийн бүхэл хэсгийн нийлбэрийг ол.
A.$-1$ B.$0$ C.$1$ D.$2$ E.$3$
Бодлогын төрөл:Сонгох
Амжилтын хувь:65.56%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:$f(x)$ нь тасралтгүй функц бөгөөд $f(z)\cdot f(z+1)< 0$ бол $f(x)=0$ тэгшитгэл $]z,z+1[$ завсарт дор хаяж нэг ширхэг шийдтэй байна. Түүнчлэн $z$ нь бүхэл тоо бол эдгээр шийдийн бүхэл хэсэг нь $z$ байна.
Бодолт:\begin{align*}
f(-1)&=(-1)^3-3(-1)^2+3=-1\\
f(0)&=0^3-3\cdot 0^2+3=3\\
f(1)&=1^3-3\cdot 1^2+3=1\\
f(2)&=2^3-3\cdot 2^2+3=-1\\
f(3)&=3^3-3\cdot 3^2+3=3
\end{align*}
тул $f(x)=0$ тэгшитгэл $]-1;0[$, $]1;2[$, $]2;3[$ засруудад шийдтэй бөгөөд эдгээр шийдүүдийн бүхэл хэсгүүдийн нийлбэр нь $-1+1+2=2$ байна.
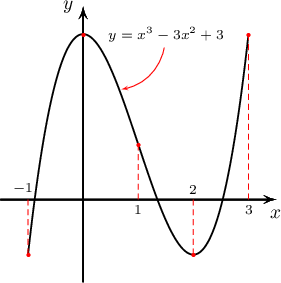Жич: Дурын куб тэгшитгэлийн шийдүүдийг аль завсарт байрлахыг тогтоох нь амаргүй бодлого юм. Энэ бодлогын тухайд $f(x)$-ийн графикийг байгуулж шийдүүдийг баримжаалсан болно.