Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Шулуунуудын огтлолцлын цэг, хоорондох өнцөг
$\ell\colon y=px-3\ (p>0)$, $m\colon y=\dfrac12x+2$ шулуунуудын огтлолцолын цэгийг $C$, $x$ тэнхлэгтэй огтлолцох цэгүүдийг нь $A$, $B$ гэе. $S_{ABC}=\dfrac{15}{2}$ бол $p=\fbox{a}$ байна. Энэ үед $\ell$, $m$ шулуунуудын $x$ тэнхлэгтэй үүсгэх өнцгийг $\alpha$, $\beta$ гэвэл $\tg\alpha=\fbox{b}$, $\tg\beta=\dfrac{\fbox{c}}{\fbox{d}}$ болно. Иймд эдгээр шулуунуудын хоорондох хурц өнцөг $\gamma=\dfrac{\pi}{\fbox{e}}$ байна.
a = 3
b = 3
cd = 12
e = 4
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 50.05%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $\left\{\begin{array}{c} y=px-3\\ y=\frac12x+2\end{array}\right.$ систем тэгшитгэлийг бодож огтлолцлийн цэг $C$-ийн координатыг олно. Энэ цэгийн $y$ координат нь $ABC$ гурвалжны өндөр болох ба $AB$ талын урт нь $\ell$, $m$ шулуунуудын $x$ тэнхлэгийг огтлох цэгүүдийн хоорондох зай байна. Мөн $p>0$ ба бүхэл тоо гарах ёстой тул $p\ge 1$ гэж үзэж болно.
Бодолт: Огтлолцлын цэгийн координат нь:
$$\left\{\begin{array}{c} y=px-3\\ y=\frac12x+2\end{array}\right.\Rightarrow (p-\tfrac12)x-5=0\Rightarrow x=\dfrac{10}{2p-1},\ y=\dfrac{4p+3}{2p-1}$$
байна. $p\ge 1$ бүхэл тоо гэж үзэж болох тул $y>0$ байна.
$\ell$ шулууны $x$ тэнхлэгтэй огтлолцох цэгийн абсцисс нь $0=px-3\Rightarrow x=\dfrac3p$, $m$ шулууны $x$ тэнхлэгтэй огтлолцох цэгийн абсцисс нь $0=\frac12x+2\Rightarrow x=-4$ тул $$AB=\left|\frac3p-(-4)\right|=\frac{4p+3}{p}$$ байна. $ABC$ гурвалжны $C$ оройгоос татсан өндөр $\dfrac{4p+3}{2p-1}$ тул талбай нь $$\dfrac12\cdot\frac{4p+3}{p}\cdot\dfrac{4p+3}{2p-1}=\dfrac{15}{2}\Leftrightarrow 14p^2-39p-9=0$$ байна. Тэгшитгэлийг бодож эерэг шийдийг нь авбал $p=3$ болно. Шулууны өнцгийн коэффициент нь уг шулууны $x$ тэнхлэгтэй үүсгэх өнцгийн тангес байдаг тул $\tg\alpha=3$, $\tg\beta=\dfrac12$ байна. Хоёр шулууны хооронд үүсэх өнцөг нь $\gamma=\alpha-\beta$ ба $$\tg\gamma=\dfrac{\tg\alpha-\tg\beta}{1+\tg\alpha\cdot\tg\beta}=\dfrac{3-\frac12}{1+3\cdot \frac12}=1$$ тул $\gamma=45^\circ$ байна.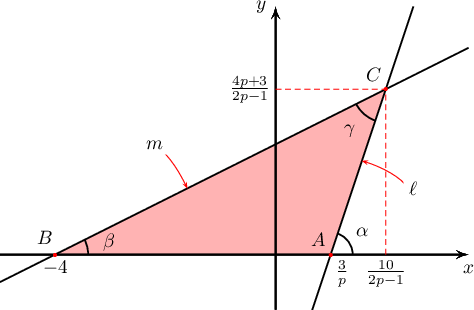
$\ell$ шулууны $x$ тэнхлэгтэй огтлолцох цэгийн абсцисс нь $0=px-3\Rightarrow x=\dfrac3p$, $m$ шулууны $x$ тэнхлэгтэй огтлолцох цэгийн абсцисс нь $0=\frac12x+2\Rightarrow x=-4$ тул $$AB=\left|\frac3p-(-4)\right|=\frac{4p+3}{p}$$ байна. $ABC$ гурвалжны $C$ оройгоос татсан өндөр $\dfrac{4p+3}{2p-1}$ тул талбай нь $$\dfrac12\cdot\frac{4p+3}{p}\cdot\dfrac{4p+3}{2p-1}=\dfrac{15}{2}\Leftrightarrow 14p^2-39p-9=0$$ байна. Тэгшитгэлийг бодож эерэг шийдийг нь авбал $p=3$ болно. Шулууны өнцгийн коэффициент нь уг шулууны $x$ тэнхлэгтэй үүсгэх өнцгийн тангес байдаг тул $\tg\alpha=3$, $\tg\beta=\dfrac12$ байна. Хоёр шулууны хооронд үүсэх өнцөг нь $\gamma=\alpha-\beta$ ба $$\tg\gamma=\dfrac{\tg\alpha-\tg\beta}{1+\tg\alpha\cdot\tg\beta}=\dfrac{3-\frac12}{1+3\cdot \frac12}=1$$ тул $\gamma=45^\circ$ байна.