Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Пирамидын эзлэхүүн
Хажуу ирмэгүүд нь 13 байх пирамидын суурь нь 6 ба 8 талтай тэгш өнцөгт байв. Эзлэхүүнийг ол.
A.96 B.188 C.192 D.196 E.260
Бодлогын төрөл:Сонгох
Амжилтын хувь:63.37%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:$V=\dfrac13S_{\text{суурь}}\cdot h$ байна.
Бодолт: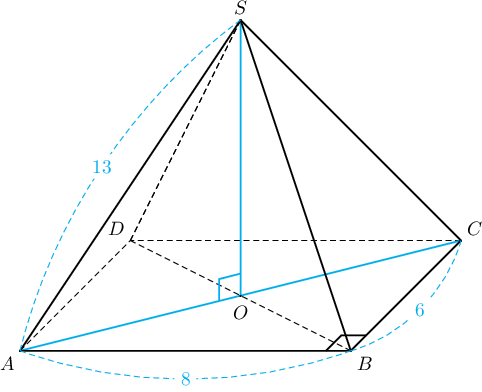
$ABC$ тэгш өнцөгт гурвалжнаас Пифагорын теоремоор $$AC^2=AB^2+BC^2=8^2+6^2=100\Rightarrow AC=10$$ байна. Тэгш өнцөгтийн диагоналиуд огтлолцлынхоо цэгээр таллан хуваагдах тул $AO=\dfrac{AC}{2}=5$ болно.
$AOS$ тэгш өнцөгт гурвалжнаас Пифагорын теоремоор $$SO^2=AS^2-AO^2=13^2-5^2=144\Rightarrow h=SO=12$$ байна.
$ABCD$ тэгш өнцөгтийн талбай $8\cdot 6=48$. Иймд $$V=\dfrac13S_{\text{суурь}}\cdot h=\dfrac13\cdot 48\cdot 12=192$$ байна.
$AOS$ тэгш өнцөгт гурвалжнаас Пифагорын теоремоор $$SO^2=AS^2-AO^2=13^2-5^2=144\Rightarrow h=SO=12$$ байна.
$ABCD$ тэгш өнцөгтийн талбай $8\cdot 6=48$. Иймд $$V=\dfrac13S_{\text{суурь}}\cdot h=\dfrac13\cdot 48\cdot 12=192$$ байна.
Сорилго
2017-10-21 2016-06-03 Сорилго 2019 №1А ЭЕШ сорил 1 эеш -2019 хувилбар Огторгуйн геометр Пирамид Огторгуйн геометр-1