Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Логарифм, тригонометр тэгштгэл, тэнцэтгэл биш
$f(x)=\log_2(1-\sin x)-\log_2(1+\sin x)$ бол
- $f\big(\frac{\pi}{4}\big)-f(\arccos\frac18)=\fbox{a}$,
- $f(x)=-1$ тэгшитгэл $x=\dfrac{\pi}{\fbox{b}}+\dfrac{\pi}{\fbox{c}}k$, $k\in\mathbb Z$
- $f(x)\le-2$ тэнцэтгэл биш $$x\in\left[\dfrac{\pi}{\fbox{d}}+2\pi k;\dfrac{\fbox{e}\pi}{3}+2\pi k\right]\cup\left[\dfrac{\fbox{g}\pi}{3}+2\pi k;\dfrac{\fbox{h}\pi}{3}+2\pi k\right],\ k\in\mathbb Z$$ шийдтэй байна.
a = 5
bc = 42
defg = 3245
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 45.65%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $$f(x)=\log_2(1-\sin x)-\log_2(1+\sin x)=\log_2(1-\sin^2x)=\log_2\cos^2x$$
байна.
Косинус нь сөрөг байж болох тул $\log_2\cos^2x=2\log_2\cos x$ тэнцэл үргэлж биелэх албагүйг анхаар.
Косинус нь сөрөг байж болох тул $\log_2\cos^2x=2\log_2\cos x$ тэнцэл үргэлж биелэх албагүйг анхаар.
Бодолт:
- $f(x)=\log_2\cos^2x$ тул $$f\Big(\frac{\pi}{4}\Big)=\log_2\cos^2\frac{\pi}{4}=\log_2\Big(\frac{\sqrt2}{2}\Big)^2=\log_2\frac12=-1,$$ $$f\Big(\arccos\frac{1}{8}\Big)=\log_2\cos^2\Big(\arccos\frac{1}{8}\Big)=\log_2\Big(\frac{1}{8}\Big)^2=\log_2\frac1{64}=-6$$ тул $f\big(\frac{\pi}{4}\big)-f(\arccos\frac18)=-1-(-6)=5$ байна.
- $\log_2\cos^2x=-1\Leftrightarrow \cos^2x=\dfrac12\Leftrightarrow\dfrac{1+\cos 2x}{2}=\dfrac12$ тул $\cos 2x=0$ байна. Иймд $$2x=\dfrac{\pi}{2}+\pi k\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{\pi}{2}k$$
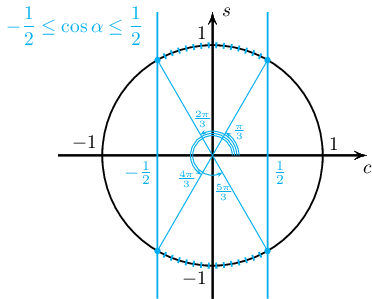
- $\log_2\cos^2x\le-2\Leftrightarrow \cos^2x\le\dfrac14\Leftrightarrow-\dfrac12\le\cos x\le\dfrac12$ тул
$$x\in\left[\dfrac{\pi}{3}+2\pi k;\dfrac{2\pi}{3}+2\pi k\right]\cup\left[\dfrac{4\pi}{3}+2\pi k;\dfrac{5\pi}{3}+2\pi k\right],\ k\in\mathbb Z$$
