Монгол Бодлогын Сан

Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.

Тойрогт багтсан $ABCD$ дөрвөн өнцөгтөд $AB=BC=4$ , $CD=5$ , $DA=9$ байв.

$\triangle ABD$ болон $\triangle BCD$ -ээс косинусын теоремоор $BD$ -г олж тэнцүүлбэл $\angle A=\fbox{ab}^\circ$ . Иймд $BD=\sqrt{\fbox{cd}}$ .
$S_{ABCD}=S_{ABD}+S_{BCD}=\fbox{ef}\cdot\sqrt{\fbox{g}}$

ab = 60

cd = 61

efg = 143

Бодлогын төрөл: Нөхөх

Амжилтын хувь: 13.45%

Заавар: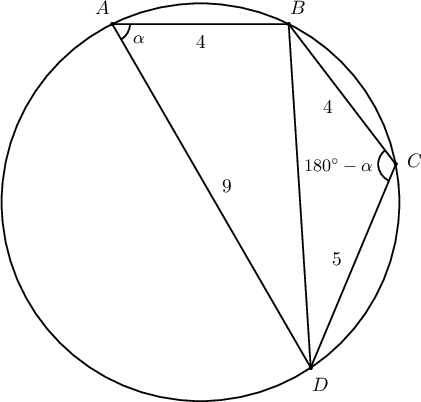

Тойрогт багтсан дөрвөн өнцөгтийн эсрэг өнцгүүдийн нийлбэр

$180^\circ$ байна.

Бодолт:

$\triangle ABD$ болон $\triangle BCD$ -ээс косинусын теоремоор $BD$ -г олж тэнцүүлбэл $AB^2+AD^2-2AB\cdot AD\cos\alpha=BC^2+CD^2-2BC\cdot CD\cos(180^\circ-\alpha)$ тул $4^2+9^2-2\cdot 4\cdot 9\cos\alpha=4^2+5^2+2\cdot 4\cdot 5\cos\alpha$ болох ба эндээс $\cos\alpha=\dfrac{9^2-5^2}{2\cdot 4\cdot 14}=\dfrac12$ болно. Иймд $\alpha=60^\circ$ ба $BD=\sqrt{4^2+9^2-2\cdot 4\cdot 9\cdot\dfrac12}=\sqrt{61}$
$\begin{align*} S_{ABCD}&=S_{ABD}+S_{BCD}=\dfrac{1}{2}AB\cdot AD\sin60^\circ+\dfrac{1}{2}BC\cdot CD\sin 120^\circ\\ &=\dfrac{1}{2}\cdot4\cdot 9\cdot\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}\cdot 4\cdot 5\cdot\dfrac{\sqrt{3}}{2}=14\sqrt{3} \end{align*}$