Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Ирмэгүүд дээр оройтой гурвалжны талбай
Бүх ирмэгийнх нь урт $6$-тай тэнцүү $OABC$ зөв тетраэдрийн $OA$, $OB$, $OC$ ирмэгүүд дээр $OL=3$, $OM=4$, $ON=2$ байхаар $L$, $M$, $N$ цэгүүд авав.
- $LM=\sqrt{\fbox{ab}}$, $MN=2\sqrt{\fbox{c}}$, $NL=\sqrt{\fbox{d}}$;
- $\sin\angle MLN=\dfrac{\fbox{e}\sqrt{\fbox{f}}}{\sqrt{91}}$;
- $S_{\triangle LMN}=\dfrac{\fbox{h}\sqrt{3}}{\fbox{i}}$ байна.
ab = 13
c = 3
d = 7
ef = 53
gh = 52
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 60.61%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Косинусын теорем ашигла:
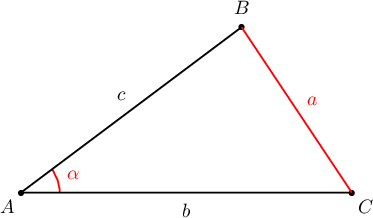$$\color{red}{a^2}=b^2+c^2-2bc\cdot\color{red}{\cos\alpha}$$
Бодолт: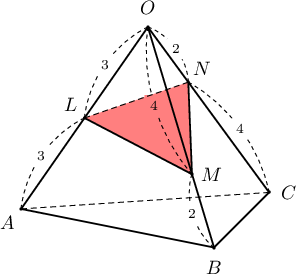 
- Косинусын теоремоор \begin{align*} LM&=\sqrt{3^2+4^2-2\cdot 3\cdot 4\cdot\dfrac12}=\sqrt{13}\\ MN&=\sqrt{4^2+2^2-2\cdot 4\cdot 2\cdot\dfrac12}=\sqrt{12}=2\sqrt{3}\\ NL&=\sqrt{2^2+3^2-2\cdot 2\cdot 3\cdot\dfrac12}=\sqrt{7} \end{align*}
- $\triangle LMN$-д косинусын теорем бичвэл $$\cos\angle MLN=\dfrac{LM^2+NL^2-MN^2}{2\cdot LM\cdot NL}=\dfrac{13+7-12}{2\cdot\sqrt{13}\cdot\sqrt{7}}=\dfrac{4}{\sqrt{91}}$$ Үндсэн адилтгал ашиглан синусыг нь олбол $$\sin\angle MLN=\sqrt{1-\Big(\dfrac{4}{\sqrt{91}}\Big)^2}=\dfrac{\sqrt{75}}{\sqrt{91}}=\dfrac{5\sqrt{3}}{\sqrt{91}}$$
- $S_{\triangle LMN}=\dfrac12\cdot LM\cdot NL\cdot\sin\angle MLN=\dfrac12\cdot\sqrt{13}\cdot\sqrt{7}\cdot\dfrac{5\sqrt{3}}{\sqrt{91}}=\dfrac{5\sqrt{3}}{2}$ байна.