Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Трапецийн диагоналийн урт
Адил хажуут $ABCD$ ($AB=CD$) трапецийн периметр $50$, $BC=9$, $AD=21$ байв. $AC$ диагоналын уртыг ол.
A.$13$ B.$14$ C.$15$ D.$16$ E.$17$
Бодлогын төрөл:Сонгох
Амжилтын хувь:79.33%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар: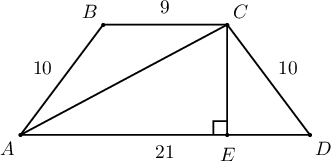
Хажуу ирмэгийн урт нь $\dfrac{50-9-21}{2}=10$ байна. $CE$ өндөр буулгаад $ACE$ тэгш өнцөгт гурвалжнаас $AC$-г ол.
Бодолт:Адил хажуут трапец тул
$$DE=\dfrac{AD-BC}{2}=\dfrac{21-9}{2}=6$$
байна. Иймд Пифагорын теоремоор $CE^2=\sqrt{10^2-6^2}=8$ байна. $AE=21-6=15$ тул $$AC^2=AE^2+CE^2=15^2+8^2=\sqrt{289}=17$$