Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Интегралаар дүрсийн талбай олох
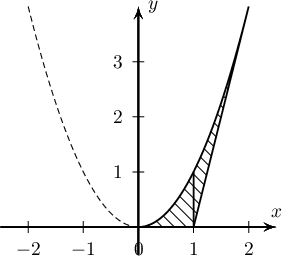
$y=x^2$ парабол ба $y=kx-k$ шулуун нь $\fbox{a}< k<\fbox{b}$ үед ерөнхий цэггүй байна. $k_1=\fbox{a}$, $k_2=\fbox{b}$ ба $\ell_1\colon y=k_1x-k_1$, $\ell_2=k_2x-k_2$ гэе. Парабол ба $\ell_1$, $\ell_2$ шулуунуудаар хүрээлэгдсэн дүрсийн талбай нь $\dfrac{\fbox{c}}{\fbox{d}}$ байна.
ab = 04
cd = 23
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 48.57%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Парабол шулуун хоёр огтлолцохгүй байхын тулд $x^2=kx-k$ тэгшитгэл шийдгүй байна.
Бодолт: $x^2=kx-k\Leftrightarrow x^2-kx+k=0$ тэгшитгэл шийдгүй байхын тулд $D=k^2-4\cdot 1\cdot k<0\Leftrightarrow 0< k< 4$ байна. $y=x^2$ парабол, $y=0$ шулуун ба $y=4x-4$ шулуунуудаар хүрээлэгдсэн дүрсийн талбай нь $$\int_{0}^1 x^2\mathrm{d}x+\int_1^2(x^2-4x+4)\mathrm{d}x=\dfrac{x^3}{3}\bigg|_0^1+\dfrac{(x-2)^3}{3}\bigg|_1^2=\dfrac13+\dfrac13=\dfrac23$$
байна.
