Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Суурийн цэгээс хажуу ирмэг хүртэлх зай
$a$ талтай $ABCD$ зөв тетраэдр (бүх ирмэгийн урт нь тэнцүү) өгөгдөв.
- $A$ оройгоос $BCD$ талд буулгасан $AH$ өндрийн урт $\dfrac{\sqrt{\fbox{a}}}{\fbox{b}}a$;
- $ABCD$ тетраэдрийн эзлэхүүн $\dfrac{\sqrt{\fbox{c}}}{\fbox{de}}a^3$
- Өндрийн суурь $H$ цэгээс $ABC$ талс хүртэлх зай $\dfrac{\sqrt{\fbox{f}}}{\fbox{g}}a$ байна.
ab = 63
cde = 212
fg = 69
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 42.40%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар:
- $BH$-ийг олоод Пифагорын теорем ашигла;
- $V=\dfrac13Sh$;
- $V_{HABC}=\dfrac13V$ болохыг ашигла.
Бодолт: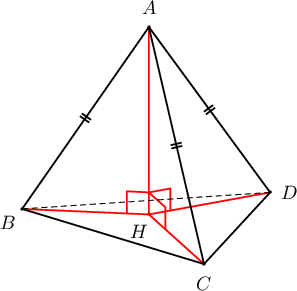 
- $BH$ нь $BCD$ гурвалжныг багтаасан тойргийн радиус байна. Иймд синусын теоремоор $$\dfrac{a}{\sin 60^\circ}=2BH\Rightarrow BH=\dfrac{a}{2\cdot\frac{\sqrt3}{2}}=\dfrac{a}{\sqrt{3}}$$ байна. Пифагорын теоремоор $$AH=\sqrt{AB^2-BH^2}=\sqrt{a^2-\dfrac{a^2}{3}}=\dfrac{\sqrt6}{3}a$$
- Суурийн талбай нь $S=\dfrac12 a^2\sin60^\circ=\dfrac{\sqrt3}{4}a^2$ тул $$V=\dfrac13Sh=\dfrac13\cdot\dfrac{\sqrt3}{4}a^2\cdot\dfrac{\sqrt6}{3}a=\dfrac{\sqrt2}{12}a^3$$
- $HABC$ пирамидын эзлэхүүн нь $V_{HABC}=\dfrac13 V=\dfrac{\sqrt2}{36}a^3$ байна. Нөгөө талаас $$V_{HABC}=\dfrac13S_{ABC}\cdot d=\dfrac13\cdot\dfrac{\sqrt3a^2}{4}\cdot d=\dfrac{\sqrt{3}a^2}{12}\cdot d$$
Иймд $\dfrac{\sqrt{3}a^2}{12}\cdot d=\dfrac{\sqrt2}{36}a^3\Rightarrow d=\dfrac{\sqrt6}{9}a$ байна.