Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Өнцөг олох
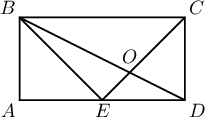
$ABCD$ тэгш өнцөгт, $AB=AE=ED$ бол $\angle COD=?$
A.$\dfrac{\pi}{18}+\arctg\dfrac12$ B.$45^\circ$ C.$100^\circ$ D.$\dfrac{\pi}{4}+\arctg\dfrac12$ E.$60^\circ$
Бодлогын төрөл:Сонгох
Амжилтын хувь:46.99%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:$O$ цэгийг дайруулан $CD$ талд перпендикуляр тат.
Бодолт:$O$ цэгийг дайруулан $CD$ талд перпендикулярын суурийг $F$ гэвэл $\angle COF=\angle CED=\dfrac{\pi}{4}$, $\angle DOF=\angle DBC=\arctg\dfrac12$ байна. Иймд $\angle COD=\dfrac{\pi}{4}+\arctg\dfrac12$ байна.
