Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Шүргэгч ба огтлогчийн чанар
$AB$-шүргэгч, $BD$-огтлогч, $\angle DOC=60^\circ$, $DC=CB$, $AB=\sqrt6$ бол $OB=?$
A.$\sqrt3$ B.$\dfrac{\sqrt3}{2}$ C.$2$ D.$1$ E.$3$
Бодлогын төрөл:Сонгох
Амжилтын хувь:46.77%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:Шүргэгч ба огтлогчийн чанар ашигла.
Бодолт: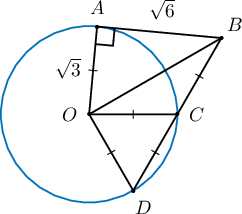
$\triangle OCD$ нь адил хажуут гурвалжин ба оройн өнцөг нь $60^\circ$ тул суурийн өнцгүүд нь $$\alpha=\dfrac{180^\circ-60^\circ}{2}=60^\circ$$
тул зөв гурвалжин байна. Иймд $$OA=OC=OD=CD=BC=R$$ ба $BD=2R$ байна. Шүргэгч ба огтлогчийн чанараар $BA^2=BC\cdot BD$ тул $$(\sqrt6)^2=R\cdot 2R\Rightarrow R=\sqrt3$$
Пифагорын теоремоор $OB^2=OA^2+BA^2$ тул $OB^2=(\sqrt3)^2+(\sqrt6)^2=9$ тул $OB=3$ байна.
Сорилго
2016-02-05 hw-56-2016-06-15 Хавтгайн геометр 2 Өмнөговь аймгийн 9 жилийн сургуулийн багш нарын сургалтанд бодох бодлогууд Хавтгайн геометр 2020-03-09 сорил ДАВТЛАГА №4, Тойрог ба олон өнцөгт ДАВТЛАГА №4, Тойрог ба олон өнцөгт тестийн хуулбар Тойрог, түүнтэй холбоотой бодлогууд ДАВТЛАГА №4, Тойрог ба олон өнцөгт тестийн хуулбар Хавтгайн геометр 2 тестийн хуулбар