Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
ЭЕШ 2008 A №58
Параллелограммын хоёр талын урт 2 ба 7, нэг диагоналийн урт 8 бол нөгөө диагоналийн уртыг ол.
A.$8$ B.$8.5$ C.$\sqrt{42}$ D.$10$ E.$\sqrt{11}$
Бодлогын төрөл:Сонгох
Амжилтын хувь:48.81%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар: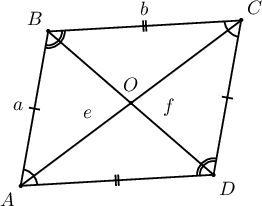
Параллелограммын талуудын уртын квадратуудын нийлбэр нь диагоналиудын уртын квадратуудын нийлбэртэй тэнцүү байна.
$$AB^2+BC^2+CD^2+DA^2=AC^2+BD^2$$
буюу
$$2(a^2+b^2)=e^2+f^2$$
байна.
Бодолт:$$2(2^2+7^2)=8^2+f^2\Rightarrow f^2=106-64=42\Rightarrow f=\sqrt{42}$$
Санамж: Параллелограммын энэхүү чанар, гурвалжны медианы уртыг олох томьёо зэргийг косинусын теорем ашиглан хялбархан баталж болдог.
Санамж: Параллелограммын энэхүү чанар, гурвалжны медианы уртыг олох томьёо зэргийг косинусын теорем ашиглан хялбархан баталж болдог.
Сорилго
2016-02-08 ЭЕШ 2008 A hw-58-2016-05-25 Косинусын теорем 2008 оны ЭЕШ-ийн онцлох бодлогууд. geometr Хавтгайн геометр Хавтгайн геометр Косинусын теорем Косинусын теорем тестийн хуулбар СИНУС БА КОСИНУСЫН ТЕОРЕМ Синус, косинусын теорем ДӨРВӨН ӨНЦӨГТ Косинус ба синусын теорем