Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
ЭЕШ 2008 A №62
Тойрогт багтсан $ABCD$ дөрвөн өнцөгтийн $AD=\sqrt3$, $CD=\sqrt2$ ба $\angle ADB=60^\circ$, $\angle CAD=45^\circ$ бол
- багтаасан тойргийн радиус $R=\fbox{a}$
- $\angle BDC=\fbox{bc}^\circ$
- $AB^2=\fbox{d}$ байна.
a =1
bc =15
d =3
Бодлогын төрөл:Нөхөх
Амжилтын хувь:26.83%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:Синусын теорем ашигла:
$$\dfrac{a}{\sin\alpha}=\dfrac{b}{\sin\beta}=\dfrac{c}{\sin\gamma}=2R$$
Бодолт: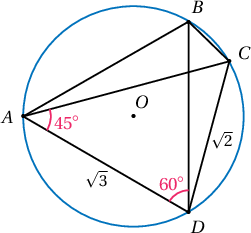
$\triangle ACD$ гурвалжны хувьд синусын теорем бичвэл $2R=\dfrac{\sqrt2}{\sin45^\circ}\Rightarrow R=1$.
Нэг нумд тулсан өнцгүүд тул $\angle BDC=\angle BAC$ байна. $\sin\angle ABD=\dfrac{AD}{2R}=\dfrac{\sqrt3}{2}$ тул $\angle ABC=60^\circ$ байна. Иймд $$\angle BAC=180^\circ-60^\circ-60^\circ=60^\circ\Rightarrow\angle BAC=60^\circ-45^\circ=15^\circ$$
$\triangle ABD$ нь зөв гурвалжин тул $AB=\sqrt3\Rightarrow AB^2=3$ байна.
Нэг нумд тулсан өнцгүүд тул $\angle BDC=\angle BAC$ байна. $\sin\angle ABD=\dfrac{AD}{2R}=\dfrac{\sqrt3}{2}$ тул $\angle ABC=60^\circ$ байна. Иймд $$\angle BAC=180^\circ-60^\circ-60^\circ=60^\circ\Rightarrow\angle BAC=60^\circ-45^\circ=15^\circ$$
$\triangle ABD$ нь зөв гурвалжин тул $AB=\sqrt3\Rightarrow AB^2=3$ байна.
Сорилго
2016-02-08 ЭЕШ 2008 A 2016-06-06 hw-56-2016-06-15 2008 оны ЭЕШ-ийн онцлох бодлогууд. Хавтгайн геометр 2 Хавтгайн геометр 3 Хавтгайн геометр 3 шинэ Синусын теорем Синус, косинусын теорем Хавтгайн геометр 2 тестийн хуулбар Косинус ба синусын теорем