Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Багтсан зөв зургаан өнцөгт
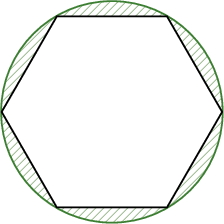
Тойрогт багтсан зөв 6 өнцөгтийн периметр 24 бол зурагт дүрслэгдсэн будагдсан хэсгийн талбайг ол.
A.$2\pi+\sqrt3$ B.$8\pi-12\sqrt3$ C.$4\pi-2\sqrt3$ D.$16\pi-24\sqrt3$ E.$24\pi-12\sqrt3$
Бодлогын төрөл:Сонгох
Амжилтын хувь:61.07%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:Дугуйн талбайгаас 6 өнцөгтийн талбайг хасаж ол.
Бодолт:Зөв зургаан өнцөгт тул багтаасан тойргийн радиус нь зургаан өнцөгтийн талын урттай тэнцүү байна. Иймд $r=\dfrac{24}{6}=4$ байна. Иймд дугуйн талбай $16\pi$ байна. Зөв зургаан өнцөгтийн талбай 4 талтай зөв гурвалжны талбайгаас 6 дахин их тул $6\cdot\dfrac{\sqrt{3}\cdot 4^2}{4}=24\sqrt3$ байна. Иймд зурааслагдсан хэсгийн талбай $$16\pi-24\sqrt3$$ байна.
Сорилго
2016-02-14 Хавтгайн геометр 1 Өмнөговь аймгийн 9 жилийн сургуулийн багш нарын сургалтанд бодох бодлогууд 2020-03-09 сорил математик101 Дунд сургуулийн геометр математик101 тестийн хуулбар Дунд сургуулийн геометр тестийн хуулбар Тойрог, түүнтэй холбоотой бодлогууд СЕКТОР СЕГМЕНТИЙН ТАЛБАЙ Хавтгайн геометр 1 тестийн хуулбар Circle Нумын урт, Сектор