Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
ЭЕШ 2008 A №91
$x=a$, $x=2a\ (0< a<2.5)$, $y=0$, $y=5+4x-x^2$ шугамуудаар хүрээлэгдсэн дүрс $a$-ийн ямар утганд хамгийн их талбайтай байх вэ?
A. $\dfrac{-6+\sqrt{71}}{7}$
B. $\dfrac{-6-\sqrt{71}}{7}$
C. $\dfrac{9-\sqrt{186}}{7}$
D. $\dfrac{-9+\sqrt{186}}{7}$
E. $\dfrac{6+\sqrt{71}}{7}$
Бодлогын төрөл: Сонгох
Амжилтын хувь: 27.70%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $x\in[-1;5]$ мужид $y=5+4x-x^2>0$ байна.
Бодолт: $a\in]0;2.5[$ үед $]a;2a[\in[-1;5]$ тул $y=5+4x-x^2>0$ байна. Иймд бидний олох дүрсийн талбай
$$S(a)=\int_a^{2a}[(5+4x-x^2)-0]\,\mathrm{d}x=\Big(5x+2x^2-\dfrac{x^3}{3}\Big)\bigg|_{a}^{2a}=$$
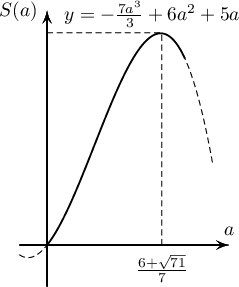
$$=\Big(10a+8a^2-\dfrac{8a^2}{3}\Big)-\Big(5a+2a^2-\dfrac{a^2}{3}\Big)=-\dfrac{7a^3}{3}+6a^2+5a$$
$S^\prime(a)=-7a^2+12a+5=0\Leftrightarrow a=\dfrac{-12\pm\sqrt{12^2-4\cdot(-7)\cdot 5}}{2\cdot(-7)}$ тул $a_1=\dfrac{6+\sqrt{71}}{7}$, $a_2=\dfrac{6-\sqrt{71}}{7}$ ба $a_1=\dfrac{6+\sqrt{71}}{7}$ нь максимумын цэг байна.
