Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Конусын дэлгээс
$AB$ нь $O$ оройтой конусын суурийн диаметр бөгөөд, уг конусын байгуулагч нь суурийн радиусаас 3 дахин урт байв. Хэрвээ суурийн радиус нь $r$, $P$ нь $BP=r$ байх $OB$ хэрчим дээрх цэг бол конусыг $OA$ байгуулагчийн дагуу дэлгэсэн дэлгээсийн төв өнцөг нь $\fbox{abc}^\circ$ байна. $A$ цэгээс конусын гадаргуугийн дагуу явж $P$ цэг хүрэх хамгийн дөт замын урт нь $\sqrt{\fbox{d}}r$ байна.
abc = 120
d = 7
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 48.86%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $R$ радиустай тойргийн $\alpha$ төв өнцөгт харгалзах нумын урт $\alpha R$ байдаг.
Хавтгай дээр хоёр цэгийг холбосон хамгийн дөт зам нь тэдгээр цэгүүдийг холбосон хэрчим юм.
Хавтгай дээр хоёр цэгийг холбосон хамгийн дөт зам нь тэдгээр цэгүүдийг холбосон хэрчим юм.
Бодолт: Байгуулагчийн урт нь $3r$ тул дэлгээсийн төв өнцөгт харгалзах нумын урт $3r\alpha$ байна. Нөгөө талаас энэ нь суурийн тойргийн урт тул $2\pi r$ байна. Иймд $\alpha=\dfrac{2\pi}{3}$ буюу $120^\circ$ өнцөг байна.
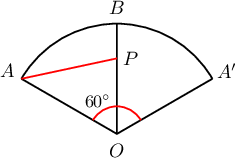Дэлгээс дээрх $\triangle OAP$-д косинусын теорем бичвэл
$$AP^2=OA^2+OP^2-2OA\cdot OP\cdot\cos60^\circ$$
$$=(3r)^2+(2r)^2-2(3r)(2r)\cdot\dfrac12=7r^2$$
тул $AP=\sqrt{7}r$ ба энэ нь $A$ цэгээс конусын гадаргуугийн дагуу явж $P$ цэг хүрэх хамгийн дөт зам байна.