Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Параболуудын хоорондох дүрсийн талбай
$y=x^2$, $y=-x^2+4x+6$ параболуудын огтлолцолд үүсэх дүрсийн талбайг ол.
A. $-10$
B. $21.3$
C. $20$
D. $\dfrac{61}{3}$
E. $\dfrac{64}{3}$
Бодлогын төрөл: Сонгох
Амжилтын хувь: 69.31%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $$\int_a^b p(x-a)(x-b)\,\mathrm{d}x=\dfrac{p(a-b)^3}{6}$$ байдаг.
$f(x)$, $g(x)$ функцүүдийн графикийн огтлолцолд үүсэх дүрсийн талбайг олохдоо график дээр орших функцийн утгаас, доор орших функцийн утгыг хасаад огтлолцлын цэгүүдийн хооронд интеграл авна.
$f(x)$, $g(x)$ функцүүдийн графикийн огтлолцолд үүсэх дүрсийн талбайг олохдоо график дээр орших функцийн утгаас, доор орших функцийн утгыг хасаад огтлолцлын цэгүүдийн хооронд интеграл авна.
Бодолт: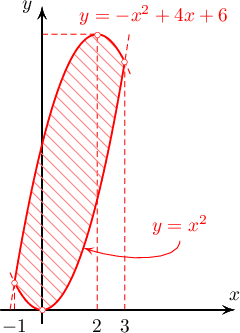 
$y=-x^2+4x+6$ функцийн утгууд нь огтлолцлын $[-1;3]$ мужид $y=x^2$ функцийн утгаас их буюу график нь дээр нь байрлаж байгаа тул огтлолцолд үүсэх дүрсийн талбай нь
$$\int_{-1}^3[(-x^2+4x+6)-x^2]\,\mathrm{d}x=\int_{-1}^3(-2)(x+1)(x-3)\mathrm{d}x$$
$$=\dfrac{(-2)(-1-3)^3}{6}=\dfrac{64}{3}$$