Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Систем тэнцэтгэл биш
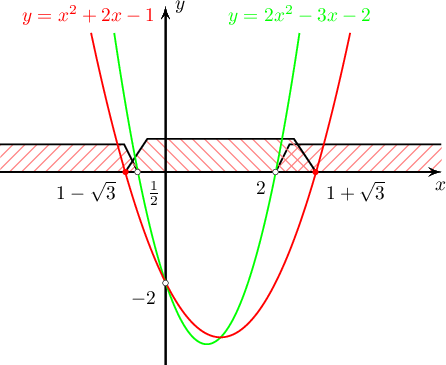
$\left\{ \begin{array}{c} 2x^2-3x > 2\\ x^2-2 \leq 2x \end{array} \right.$ тэнцэтгэл биш бод.
A. $(-\infty;-\frac12)\cup[2;+\infty)$
B. $[1-\sqrt3;1+\sqrt3)$
C. $[1-\sqrt3;-\frac12)\cup(2;3+\sqrt3]$
D. $[1-\sqrt3;-\frac12)\cup(2;1+\sqrt3]$
E. $[\frac12;\sqrt3-1)\cup(2;1+\sqrt3]$
Бодлогын төрөл: Сонгох
Амжилтын хувь: 50.00%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $a>0$ үед
$$ax^2+bx+c=a(x-x_1)(x-x_2)>0, x_1 < x_2$$
тэнцэтгэл бишийн шийд нь $]-\infty;x_1[\cup]x_2;+\infty[$,
$$ax^2+bx+c=a(x-x_1)(x-x_2)<0, x_1 < x_2$$
тэнцэтгэл бишийн шийд нь $]x_1;x_2[$ байна.
Бодолт: $$\left\{
\begin{array}{c}
2x^2-3x > 2\\
x^2-2 \leq 2x
\end{array}\right.\Leftrightarrow
\left\{\begin{array}{c}
2x^2-3x-2>0\\
x^2-2x-2 \leq 0
\end{array}
\right.$$
$$2x^2-3x-2=0\Rightarrow x_{1,2}=\dfrac{3\pm\sqrt{(-3)^2-4\cdot 2\cdot(-2)}}{2\cdot 2}=\dfrac{3\pm 5}{4}$$
тул $x_1=-\frac12$, $x_2=2$ байна. Иймд $$2x^2-3x-2>0\Leftrightarrow-\frac12 < x < 2$$ байна.
$$x^2-2x-2=0\Rightarrow x_{3,4}=\dfrac{2\pm\sqrt{(-2)^2-4\cdot1\cdot(-2)}}{2}=1\pm\sqrt{3}$$
тул $x_3=1-\sqrt3$, $x_4=1+\sqrt3$ байна. Иймд
$$x^2-2x-2 \leq 0\Leftrightarrow x\le 1-\sqrt3\cup x\ge1+\sqrt3$$
байна. Иймд тэнцэтгэл бишийн шийд нь
$$[1-\sqrt3;-\tfrac12)\cup(2;1+\sqrt3]$$
