Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Эйлер-Веннийн диаграмм
Ангийн хүүхдүүдийн 24 нь математикийн, 20 нь англи хэлний, 16 нь математик ба англи хэлний ЭЕШ өгнө. Энэ 2 шалгалтын алийг ч өгөхгүй сурагчид 4 байсан бол анги нийт хэдэн сурагчтай вэ?
A. $64$
B. $36$
C. $32$
D. $28$
E. $24$
Бодлогын төрөл: Сонгох
Амжилтын хувь: 66.67%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $A$, $B$ олонлогийн хувьд $$|A\cup B|=|A|+|B|-|A\cap B|$$ байдаг.
Үүнийг дараах (Эйлер-Веннийн) диаграммаар харвал эвтэйхэн байдаг.
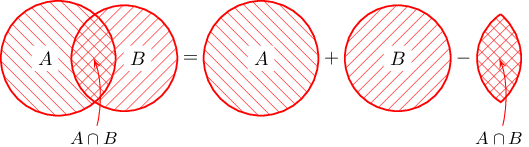
Бодолт: $A$ нь математикийн шалгалт өгөх сурагчдын олонлог, $B$ нь англи хэлний шалгалт өгөх сурагчдын олонлог гэвэл математик ба англи хэлний шалгалт өгөх сурагчдын олонлог нь $A\cap B$, энэ шалгалтын ядаж нэгийг нь өгөх сурагчдын олонлог нь $A\cup B$ байна. Иймд $$|A\cup B|=24+20-16=28$$ байна. Эдгээр сурагчид дээр 2 шалгалтын алийг ч өгөхгүй сурагчдыг нэмбэл нийт сурагчдын тоо гарах тул анги нийт $28+4=32$ сурагчтай.