Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Эзлэхүүн ба интеграл
$\ell_1: y=x^2,$ $\ell_2: y=\sqrt{x}$ муруйнууд $O(0,0)$ ба $A(x,y)$ цэгүүдэд огтолцоно.
- $x=\fbox{a} , y=\fbox{b}$
- $\ell_1$ муруйн $OA$ нумыг $OX$ тэнхлэгийг тойруулан эргүүлэхэд үүсэх биетийн эзлэхүүн $V_1=\dfrac{\pi}{\fbox{c}}$
- $\ell_2$ муруйн $OA$ нумыг $OX$ тэнхлэгийг тойруулан эргүүлэхэд үүсэх биетийн эзлэхүүн $V_2=\dfrac{\pi}{\fbox{d}}$
- $\ell_1$ ба $\ell_2$ муруйнуудын огтлолд үүсэх хавтгайн хэсгийг $OX$ тэнхлэгийг тойруулан эргүүлэхэд үүсэх биетийн эзлэхүүн $V_3=\dfrac{\fbox{e}}{\fbox{fg}}\pi$ байна.
a =1
b =1
c =5
d =2
efg =310
Бодлогын төрөл:Нөхөх
Амжилтын хувь:41.97%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:Эргэлтийн биетийн эзлэхүүн олох томьёо ашигла.
Бодолт: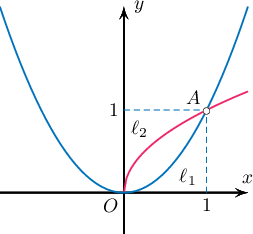
$\ell_1$ ба $\ell_2$-ын огтлолын цэгт $x^2=\sqrt{x}$ тул $x=0, x=1\Rightarrow x=1, y=1$ байна.
- $V_1=\pi\int\limits_0^1(x^2)^2 dx=\pi\dfrac{x^5}5\Big|_0^1=\dfrac{\pi}5$.
- $V_2=\pi\int\limits_0^1(\sqrt{x})^2 dx=\pi\dfrac{x^2}2\Big|_0^1=\dfrac{\pi}2$.
- $V_3=V_2-V_1=\dfrac{3}{10}\pi$.
Сорилго
2016-03-16 2017-02-03 Функц, Уламжлал, Интеграл 2 интеграл Функц, Уламжлал, Интеграл 2 тестийн хуулбар