Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Төсөөгийн харьцаа
$\triangle ABC$ гурвалжны талуудын урт нь $AB=8$, $AC=12$, $BC=16$. $D$, $E$ нь харгалзан $AB$ ба $AC$ талууд дээр орших цэгүүд бөгөөд $DE\parallel BC$ байв. Хэрвээ $BD+EC=5$ бол $DE=\fbox{ab}$ ба $S_{\triangle ADE}=\dfrac{\fbox{cd}\sqrt{\fbox{ef}}}{\fbox{g}}$ байна.
ab = 12
cdefg = 27154
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 55.60%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Төсөөгийн харьцаа бичээд
$$\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+kc}{b+kd}$$
пропорцийн чанар ашигла.
Талбайг Героны томьёо ашиглан олоорой.
Талбайг Героны томьёо ашиглан олоорой.
Бодолт: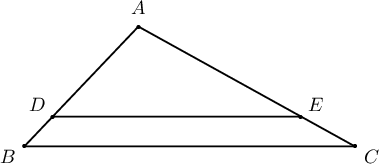 
$\triangle ABC\sim\triangle ADE$ тул $$\dfrac{AD}{AB}=\dfrac{AE}{AC}=\dfrac{DE}{BC}$$ байна. Иймд пропорцийн чанараар
$$\dfrac{AD}{AB}=\dfrac{AE}{AC}\Leftrightarrow\dfrac{AC}{AB}=\dfrac{AE}{AD}=\dfrac{AC-AE}{AB-AD}=\dfrac{EC}{BD}$$
болно. Эндээс
$$\dfrac{EC}{AC}=\dfrac{DB}{AB}=\dfrac{DB+EC}{AB+AC}=\dfrac{5}{8+12}=\dfrac{1}{4}$$
тул $AC=4EC$ байна. Иймд $AE=3EC$ болно. Өмнө бичсэн төсөөгийн харьцаагаар
$$\dfrac{AD}{AB}=\dfrac{DE}{BC}=\dfrac{AE}{AC}=\dfrac{3EC}{4EC}=\dfrac{3}{4}$$
болох тул $AD=\dfrac34\cdot 8=6$, $AE=\dfrac34\cdot 12=9$, $DE=\dfrac{3}{4}\cdot 16=12$
байна.
$p=\dfrac{6+9+12}{3}=\dfrac{27}{2}$, $p-a=\dfrac{27}{2}-6=\dfrac{15}{2}$, $p-b=\dfrac{27}{2}-9=\dfrac{9}{2}$, $p-c=\dfrac{27}{2}-12=\dfrac{3}{2}$ тул Героны томьёо ёсоор $$S_{\triangle ADE}=\sqrt{\dfrac{27}{2}\cdot \dfrac{15}{2}\cdot \dfrac{9}{2}\cdot \dfrac{3}{2}}=\dfrac{27\sqrt{15}}{4}$$
$p=\dfrac{6+9+12}{3}=\dfrac{27}{2}$, $p-a=\dfrac{27}{2}-6=\dfrac{15}{2}$, $p-b=\dfrac{27}{2}-9=\dfrac{9}{2}$, $p-c=\dfrac{27}{2}-12=\dfrac{3}{2}$ тул Героны томьёо ёсоор $$S_{\triangle ADE}=\sqrt{\dfrac{27}{2}\cdot \dfrac{15}{2}\cdot \dfrac{9}{2}\cdot \dfrac{3}{2}}=\dfrac{27\sqrt{15}}{4}$$