Монгол Бодлогын Сан

Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.

$y=\dfrac{1-x^3}{x}$ муруйн $x_0=-1$ абсцисстай цэгт татсан шүргэгчийн координатын тэнхлэгүүдтэй үүсгэх гурвалжны талбайг ол.

$\dfrac94$ B.

$\dfrac92$ C.

$4$ D.

$6$ E.

$3$

Бодлогын төрөл: Сонгох

Амжилтын хувь: 59.02%

Заавар:

$y=f(x)$ функцийн

$(x_0;f(x_0))$ цэгт татсан шүргэгч шулууны тэгшитгэл нь

$y=f^\prime(x_0)(x-x_0)+f(x_0)$ байна. Шүргэгчийн

$OX$ тэнхлэгийн эерэг чиглэлтэй үүсгэх өнцөг

$\alpha$ бол

$\tg\alpha=f^\prime(x_0)$ байна. Энэ тоо нь уг шулууны өнцгийн коэффициент болно.

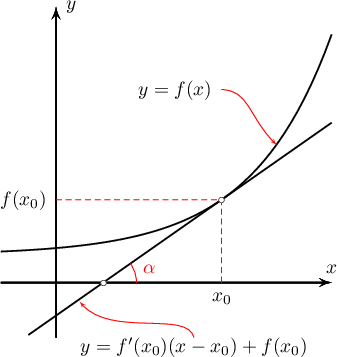
$y=kx+b$ шулуун

$\big(-\frac{b}{k};0\big)$ цэгээр

$OX$ тэнхлэгтэй огтлолцох ба

$(0;b)$ цэгээр

$OY$ тэнхлэгтэй огтлолцоно.

Бодолт:

$y^\prime=\Big(\dfrac{1}{x^2}-x\Big)^\prime=\dfrac{-2}{x^3}-1$ тул

$y(-1)=\dfrac{1-(-1)^3}{(-1)^2}=2$ ба

$y^\prime(-1)=\dfrac{-2}{(-1)^3}-1=1$ байна. Иймд шүргэгчийн тэгшитгэл нь

$y=1\cdot(x+1)+2=x+3$ болно. Энэ шулуун нь

$(-3;0)$ ,

$(0;3)$ цэгүүдэд координатын тэнхлэгийг огтлох тул талбай нь

$\dfrac{3\cdot 3}{2}=\dfrac92$ байна.