Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Гадаад шүргэлцсэн тойргууд
$3r$ радиустай $C_1$ тойрог, $r$ радиустай $C_2$ тойрогтой гадаад байдлаар $A$ цэгт шүргэлцэнэ. $A$ цэгийг үл дайрах $\ell$ шулуун $C_1$ тойргийг $B$ цэгт, $C_2$ тойргийг $C$ цэгт шүргэх бол
- $BC=\fbox{a}\sqrt{\fbox{b}}r$;
- $\measuredangle BAC=\dfrac{\pi}{\fbox{c}}$;
- $AB=\fbox{d}r$;
- $AC=\sqrt{\fbox{e}}r$;
- $S_{ABC}=\dfrac{\fbox{f}\sqrt{\fbox{g}}}{\fbox{h}}r^2$
ab = 23
c = 2
d = 3
e = 3
fgh = 332
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 54.18%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $A$ цэгээс $\ell$ шулуун хүртэлх зайг ол.
Бодолт: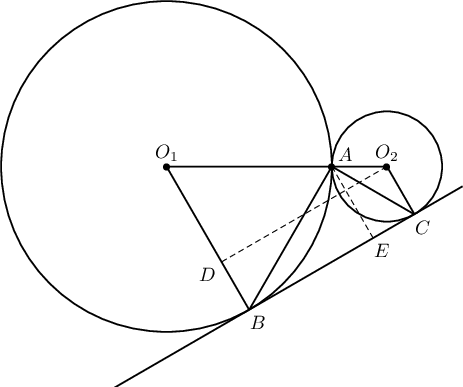 
- $BC^2=O_1O_2^2-O_1O^2=(3r+r)^2-(3r-r)^2=12r^2$ тул $BC=2\sqrt3r$.
- Хэрэв $\angle AO_1B=\alpha$ гэвэл $\angle O_1AB=\dfrac{\pi}{2}-\dfrac{\alpha}{2}$, $\angle AO_2C=\pi-\alpha$, $\angle O_2AC=\dfrac{\alpha}{2}$ байна. Иймд $$\angle BAC=\pi-(\angle O_1AB+\angle O_2AC)=\dfrac{\pi}{2}$$ байна.
- $$\dfrac{AE-r}{r}=\dfrac{3r-AE}{3r}\Rightarrow$$ $$3AE-3r=3r-AE\Rightarrow 4AE=6r\Rightarrow AE=\dfrac32r$$ $$BE=\dfrac34BC=\dfrac{3}{4}\cdot 2\sqrt3r=\dfrac{3\sqrt3}{2}r$$ $$AB^2=\sqrt{BE^2+AE^2}=\sqrt{\dfrac{27}{4}r^2+\dfrac{9}{4}r^2}=3r$$ $$AC=\sqrt{BC^2-AB^2}=\sqrt{12r^2-9r^2}=\sqrt3r$$
- $$S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{3\sqrt3}{2}r^2$$