Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Багтсан дөрвөн өнцөгт
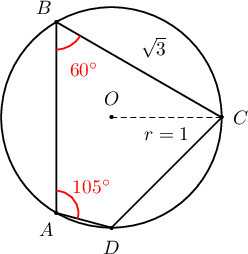
1 радиустай тойрогт багтсан $ABCD$ дөрвөн өнцөгтийн хувьд $\angle ABC=60^\circ, \angle DAB=105^\circ, |BC|=\sqrt3$ бол
- $\angle BCA=\fbox{ab}^\circ$ /1 оноо/
- $\angle CAD=\fbox{cd}^\circ$ /2 оноо/
- $|CD|=\sqrt{\fbox{e}}$ /2 оноо/
- $|AD|=\dfrac{\sqrt{\fbox{f}}-\sqrt{\fbox{e}}}{\fbox{h}}\,\,\, $ /2 оноо/
ab = 60
cd = 45
e = 2
fgh = 622
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 16.59%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Синусын теорем ашиглан $AC=\sqrt3$ болохыг харуулаад $ABC$ зөв гурвалжин гэдгийг хар.
Бодолт: Синусын теоремоор $AC=2R\sin\angle ABC=2\cdot 1\cdot\dfrac{\sqrt3}{2}=\sqrt3$. Иймд $\triangle ABC$ нь $AC=BC$ адил хажуут гурвалжин болох бөгөөд суурийн өнцөг нь $60^\circ$ тул зөв гурвалжин болно. Иймд $\angle BCA=60^\circ$ байна. $\angle CAD=105^\circ-60^\circ=45^\circ$. Синусын теоремоор
$$CD=2R\sin\angle CAD=2\cdot 1\cdot\sin45^\circ=2\cdot\dfrac{\sqrt2}{2}=\sqrt{2}$$
Тойрогт багтсан 4 өнцөгтийн эсрэг оройнууд дахь өнцгүүдийн нийлбэр $180^\circ$ тул $$\angle CDA=180^\circ-60^\circ=120^\circ$$
Иймд $ADC$ гурвалжнаас $$\angle ACD=180^\circ-\angle CAD-\angle CDA=15^\circ$$
Синусын теоремоор $$AD=2\cdot 1\cdot\sin15^\circ=2\cdot\sin(45^\circ-30^\circ)=$$
$$=2\cdot\Big(\dfrac{\sqrt2}{2}\cdot\dfrac{\sqrt3}{2}-\dfrac{\sqrt2}{2}\cdot\dfrac{1}{2}\Big)=\dfrac{\sqrt6-\sqrt2}{2}$$