Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
ЭЕШ 2016 C №27
$y=0$ шулуун ба $y=2x^2-2$ муруйгаар хязгаарлагдсан дүрсийн талбайг олоорой!
A.$4$ B.$1$ C.$2$ D.$\dfrac{8}{3}$ E.$3$
Бодлогын төрөл:Сонгох
Амжилтын хувь:36.78%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
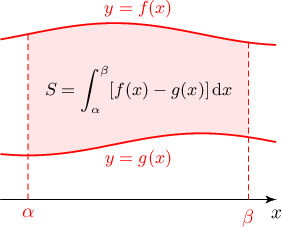
Заавар:$x\in[\alpha,\beta]$ мужид $f(x)\ge g(x)$ бол $f(x)$ ба $g(x)$ функцийн график ба $x=\alpha$, $x=\beta$ шулуунуудаар зааглагдсан дүрсийн талбай нь:
$$\int_{\alpha}^{\beta}[f(x)-g(x)]\,\mathrm{d}x$$
байна.
Бодолт:$$S=\int_{-1}^1(2-2x^2)\,\mathrm{d}x=(2x-\frac23x^3)\bigg|_{-1}^{1}=\dfrac{8}{3}$$