Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
ЭЕШ 2016 D №36
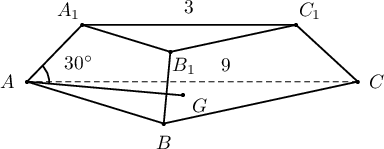
Огтлогдсон зөв гурвалжин пирамидын дээд суурийн тал 3см, доод суурийн тал 9см урттай ба хажуу ирмэг суурийн хавтгайтай $30^\circ$ өнцөг үүсгэдэг бол уг огтлогдсон пирамидын эзлэхүүнийг олоорой.
A. $\dfrac{26}{\sqrt3}$
B. $\dfrac{79}{2\sqrt3}$
C. $7\sqrt3$
D. $\dfrac{117}{2\sqrt3}$
E. $\dfrac{79}{3\sqrt3}$
Бодлогын төрөл: Сонгох
Амжилтын хувь: 25.81%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Огтлогдсон пирамидын эзлэхүүн:
$$V=\dfrac13\cdot H\cdot(S_1+\sqrt{S_1S_2}+S_2)$$
$a$ талтай зөв гурвалжны талбай: $$S=\dfrac{\sqrt3 a^2}{4}$$
$a$ талтай зөв гурвалжны оройгоос төв хүртэлх зай: $$d=\dfrac{\frac{a}{2}}{\cos30^\circ}=\dfrac{\sqrt3a}{3}$$
$a$ талтай зөв гурвалжны талбай: $$S=\dfrac{\sqrt3 a^2}{4}$$
$a$ талтай зөв гурвалжны оройгоос төв хүртэлх зай: $$d=\dfrac{\frac{a}{2}}{\cos30^\circ}=\dfrac{\sqrt3a}{3}$$
Бодолт: 
$9$ талтай зөв гурвалжны оройгоос төв хүртэлх зай $AG=\dfrac{\sqrt3\cdot 9}{3}=3\sqrt3$ ба энэ гурвалжнаар сууриа хийсэн хажуу ирмэг нь суурьтай $30^\circ$ өнцөг үүсгэх пирамидын өндөр нь
$$HG=3\sqrt3\cdot\tg30^\circ=3\sqrt3\cdot\dfrac{1}{\sqrt3}=3$$
$3$ талтай зөв гурвалжны оройгоос төв хүртэлх зай $\dfrac{\sqrt3\cdot 3}{3}=\sqrt3$ ба энэ гурвалжнаар сууриа хийсэн хажуу ирмэг нь суурьтай $30^\circ$ өнцөг үүсгэх пирамидын өндөр нь
$$HG_1=\sqrt3\cdot\tg30^\circ=\sqrt3\cdot\dfrac{1}{\sqrt3}=1$$
Иймд огтлогдсон пирамидын өндөр нь $HH_1=3-1=2$ байна.
Сууриудын талбай нь $S_1=\dfrac{\sqrt3\cdot 3^2}{4}=\dfrac{9\sqrt3}{4}$, $S_2=\dfrac{\sqrt3\cdot 9^2}{4}=\dfrac{81\sqrt3}{4}$ тул эзлэхүүн нь $$V=\dfrac13\cdot2\cdot\left(\dfrac{9\sqrt3}{4}+\sqrt{\dfrac{9\sqrt3}{4}\cdot\dfrac{81\sqrt3}{4}}+\dfrac{81\sqrt3}{4}\right)=\dfrac{117}{2\sqrt3}$$
Сууриудын талбай нь $S_1=\dfrac{\sqrt3\cdot 3^2}{4}=\dfrac{9\sqrt3}{4}$, $S_2=\dfrac{\sqrt3\cdot 9^2}{4}=\dfrac{81\sqrt3}{4}$ тул эзлэхүүн нь $$V=\dfrac13\cdot2\cdot\left(\dfrac{9\sqrt3}{4}+\sqrt{\dfrac{9\sqrt3}{4}\cdot\dfrac{81\sqrt3}{4}}+\dfrac{81\sqrt3}{4}\right)=\dfrac{117}{2\sqrt3}$$