Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
ЭЕШ 2016 B №29
$\sin\left(3x-\dfrac{\pi}{6}\right)\cos\left(3x-\dfrac{\pi}{6}\right)<\dfrac{\sqrt2}{4}$ тэнцэтгэл бишийг бод.
A. $\left]\dfrac{2k\pi}{3}-\dfrac{7\pi}{24};\dfrac{11\pi}{24}+\dfrac{2k\pi}{3}\right[$
B. $\left]\dfrac{2k\pi}{3}-\dfrac{7\pi}{48};\dfrac{11\pi}{48}+\dfrac{2k\pi}{3}\right[$
C. $\left]\dfrac{2k\pi}{3}-\dfrac{11\pi}{72};\dfrac{7\pi}{72}+\dfrac{2k\pi}{3}\right[$
D. $\left]\dfrac{k\pi}{3}-\dfrac{11\pi}{72};\dfrac{7\pi}{72}+\dfrac{2k\pi}{3}\right[$
E. $\left]\dfrac{k\pi}{2}-\dfrac{11\pi}{72};\dfrac{7\pi}{72}+\dfrac{k\pi}{2}\right[$
Бодлогын төрөл: Сонгох
Амжилтын хувь: 39.77%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $2\sin\alpha\cos\alpha=\sin2\alpha$ томьёо ашиглан хялбарчил.
Бодолт: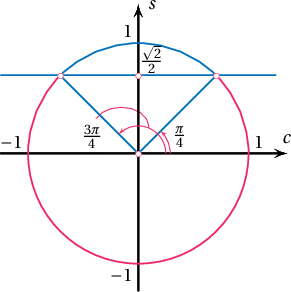 
$$\sin\Big(3x-\frac{\pi}{6}\Big)\cos\Big(3x-\frac{\pi}{6}\Big)<\frac{\sqrt2}{4}\Leftrightarrow2\sin\Big(3x-\frac{\pi}{6}\Big)\cos\Big(3x-\frac{\pi}{6}\Big)<\frac{\sqrt2}{2}\Leftrightarrow$$
$$\sin\Big(6x-\frac{\pi}{3}\Big)<\dfrac{\sqrt2}{2}$$
тул
$$\dfrac{3\pi}{4}+2\pi (k-1)<6x-\dfrac{\pi}{3}<\dfrac{\pi}{4}+2\pi k\Leftrightarrow-\dfrac{11\pi}{12}+2\pi k<6x<\dfrac{7\pi}{12}+2\pi k\Leftrightarrow$$
$$-\dfrac{11\pi}{72}+\dfrac{\pi k}{3}< x<\dfrac{7\pi}{72}+\dfrac{\pi k}{3}$$
тул $x\in\left]\dfrac{k\pi}{3}-\dfrac{11\pi}{72};\dfrac{7\pi}{72}+\dfrac{k\pi}{3}\right[$ байна.
Сорилго
ЭЕШ 2016 B
Алгебр сэдвийн давтлага 1
Алгебр сэдвийн давтлага 1
Алгебр сэдвийн давтлага 1 тестийн хуулбар