Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Хоёр шулууны хоорондох өнцөг
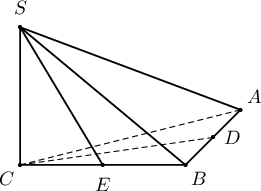
$ABC$ зөв гурвалжин суурьтай $SABC$ пирамидын суурийн талууд нь $4\sqrt2$см, $SC$ хажуу ирмэгийн урт нь $2$см бөгөөд суурийн хавтгайд перпендикуляр байв. $S$ орой ба $BC$ талын дундаж цэгийг дайрсан шулуун, $AB$ талын дундаж цэг ба $C$ оройг дайрсан шулуунуудын хоорондох өнцөг ба хоорондох зайг олоорой.
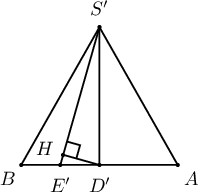
Бодолт. $AB$, $CB$ талын дундаж цэгүүдийг харгалзан $D$, $E$ гэе. $AB$ шулууныг агуулсан, $CD$ шулуунд перпендикуляр хавтгайд $SABC$ пирамидыг проекцлон $CD$ хэрчим $D^\prime$ цэгт, $E$ цэг $E^\prime$ цэгт, $S$ цэг $S^\prime$ цэгт тус тус буусан гэж үзвэл $S^\prime D^\prime\perp AB$ ба $S^\prime D^\prime=2$ болно. Бидний олох ёстой 2 шулууны хоорондох зай нь $S^\prime D^\prime E^\prime$ гурвалжны $S^\prime E^\prime$ гипотенуз дээр буусан $D^\prime H$ өндөр юм. $E^\prime D^\prime=\sqrt{\fbox{a}}$; $S^\prime E^\prime=\sqrt{\fbox{b}}$; $D^\prime H=\dfrac{\fbox{c}}{\sqrt{\fbox{d}}}$. Олох ёстой өнцгөө $\alpha$ гэж тэмдэглэвэл $SE=\fbox{e}\sqrt{\fbox{f}}$ тул $\sin\alpha=\dfrac{\sqrt{\fbox{g}}}{2}\Rightarrow\alpha=\dfrac{\pi}{\fbox{h}}$ байна.
Бодолт
$E$ цэгийг дайруулж $CD$-тай параллель шулуун татахад уг шулуун дээр $E^\prime$ цэг оршино.
Бидний олох зай нь $CD$ шулууны дурын цэгээс $(SEE^\prime)$ хавтгай хүртэлх зай байна. $SS^\prime$ хэрчмийн дундаж цэг $S^{\prime\prime}$ гэвэл $\alpha=\measuredangle S^{\prime\prime}E^\prime E$ байна.