Монгол Бодлогын Сан

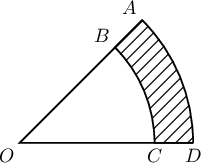
Заавар: $\measuredangle AOD$ тул секторуудын талбай нь дугуйн талбайн $\dfrac{45^\circ}{360^\circ}=\dfrac18$ байна. Дугуйн талбайг $\pi r^2$ томъёогоор боддог.

Бодолт: Жижиг секторын талбай нь $\dfrac18\pi\cdot (7\sqrt2)^2=\dfrac{49}{4}\pi$. Том секторын радиус нь $7\sqrt2+2\sqrt2=9\sqrt2$ тул талбай нь $\dfrac{1}{8}\pi\cdot(9\sqrt2)^2=\dfrac{81}{4}\pi$ байна. Иймд хар хэсгийн талбай нь $$\dfrac{81-49}{4}\cdot\pi=\dfrac{32}{4}\cdot\pi=8\pi.$$