Монгол Бодлогын Сан

Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.

$AOD$ ба

$BOC$ нь нэг төвтэй тойргийн секторууд ба

$\measuredangle AOD=30^\circ$ болно. Хэрэв

$OB=7\sqrt2$ ба

$AB=2\sqrt2$ бол харлуулсан хэсгийн талбай нь:

$7\pi$ B.

$3\pi$ C.

$\dfrac{8\pi}{3}$ D.

$\dfrac{16\pi}{3}$ E.

$5\pi$

Бодлогын төрөл: Сонгох

Амжилтын хувь: 55.56%

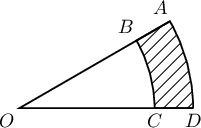
Заавар:

$\measuredangle AOD$ тул секторуудын талбай нь дугуйн талбайн

$\dfrac{30^\circ}{360^\circ}=\dfrac{1}{12}$ байна. Дугуйн талбайг

$\pi r^2$ томъёогоор боддог.

Бодолт: Жижиг секторын талбай нь

$\dfrac1{12}\pi\cdot (7\sqrt2)^2=\dfrac{49}{6}\pi$ . Том секторын радиус нь

$7\sqrt2+2\sqrt2=9\sqrt2$ тул талбай нь

$\dfrac{1}{12}\pi\cdot(9\sqrt2)^2=\dfrac{27}{3}\pi$ байна. Иймд хар хэсгийн талбай нь

$\dfrac{81-49}{6}\cdot\pi=\dfrac{16\pi}{3}$