Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Өндрүүдийн огтлолцол
$ABC$ гурвалжны $AH_1$, $BH_2$ өндрүүд $H$ цэгт огтлолцсон ба $\measuredangle BAC=60^\circ$, $\measuredangle CBA=40^\circ$, $\measuredangle ACB=80^\circ$ бол $BH:HH_2$ харьцаа аль нь вэ?
A.$\dfrac{2\cos40^\circ}{\cos80^\circ}$ B.$\dfrac{\cos40^\circ}{2\cos80^\circ}$ C.$\dfrac{2}{2\cos80^\circ-1}$ D.$\dfrac{2}{2\sin80^\circ+1}$ E.$2.5$
Бодлогын төрөл:Сонгох
Амжилтын хувь:12.90%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар: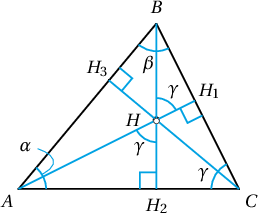
$\angle HBH_1=\angle HAH_2=90^\circ-\gamma$ тул $\angle H_1HB=\angle H_2HA=\gamma$ байна. Иймд
\begin{gather*}
BH=\dfrac{BH_1}{\sin\gamma}=\dfrac{AB\cos\beta}{\sin\gamma},\\
HH_2=\dfrac{AH_2}{\tg\gamma}=\dfrac{AB\cos\alpha\cos\gamma}{\sin\gamma}
\end{gather*}
Бодолт:\begin{gather*}
BH=\dfrac{BH_1}{\sin\gamma}=\dfrac{AB\cos\beta}{\sin\gamma},\\
HH_2=\dfrac{AH_2}{\tg\gamma}=\dfrac{AB\cos\alpha\cos\gamma}{\sin\gamma}
\end{gather*}
тул
\begin{align*}
BH:HH_2&=\dfrac{AB\cos\beta}{\sin\gamma}:\dfrac{AB\cos\alpha\cos\gamma}{\sin\gamma}\\
&=\dfrac{\cos\beta}{\cos\alpha\cos\gamma}=\dfrac{\cos40^\circ}{\cos60^\circ\cos80^\circ} \\
&=\dfrac{2\cos40^\circ}{\cos80^\circ}& & \color{WildStrawberry}{\leftarrow \cos60^\circ=\dfrac12}\
\end{align*}
Сорилго
Сорилго №1Б Геометр сэдвийн давтлага 2 ЭЕШ сорилго №20Б Гурвалжны өндөр Геометр сэдвийн давтлага 2 тестийн хуулбар