Монгол Бодлогын Сан

Заавар:Катетуудын урт нь $a$ ба $b$, гипотенузын урт нь $c$ байх тэгш өнцөгт гурвалжинд багтсан тойргийн радиус $$r=\dfrac{a+b-c}{2}$$ байдаг. Үнэндээ тойргийн гадна орших цэгээс тойрогт татсан шүргэгчийн уртууд тэнцүү тул $z+x=b$, $z+y=a$, $x+y=c$ ба тэгш өнцөгт гурвалжны хувьд $r=z$ байна.

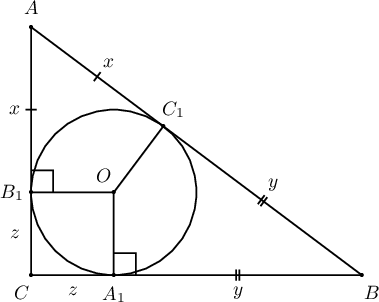
$a,b$-катет, $c$-гипотенузтай тэгш өнцөгт гурвалжныг багтаасан тойргийн радиус нь $R=\dfrac{c}{2}$.

Бодолт:$a+b+c=12$, $\dfrac ab=\dfrac{5}{12}$, $a^2+b^2=c^2$ болно. $R+r$ нь $\dfrac{a+b}{2}$ байна. $b=2.4a$ тул $a^2+(2.4a)^2=(2.6a)^2=c^2$ ба $b,c>0$ тул $c=2.6a$ байна. Иймд $a+2.4a+2.6a=12$ буюу $a=2$, $b=2.4\cdot 2=4.8$ тул $$R+r=\dfrac{4.8+2}{2}=3.4$$