Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Хамгийн их эзлэхүүнтэй багтсан цилиндр
$R$ радиустай бөмбөрцөгт багтсан хамгийн их эзлэхүүнтэй цилиндрийн хажуу гадаргууг ол.
A. $\dfrac{4\sqrt2\pi R^2}{3}$
B. $\dfrac{\pi R^2}{\sqrt2}$
C. $\dfrac{\pi R^2}{\sqrt3}$
D. $\dfrac{\pi R^2}{\sqrt3}$
E. $\pi R^2$
Бодлогын төрөл: Сонгох
Амжилтын хувь: 25.00%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: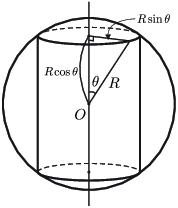 
$\theta$ ба $R$-ээр хажуу гадаргуу ба эзлэхүүнийг илэрхийл.
Бодолт: Цилиндрийн байгуулагч болон төвийг суурийн тойргийн цэгтэй холбоход үүсэх хэрчим хоёрын хоорондох өнцгийг $\theta$ гэвэл суурийн радуис нь $r=R\sin\theta$, өндөр нь $h=2R\cos\theta$ байна.
Эзлэхүүн нь $$V=S_{суурь}\cdot h=\pi r^2h=4\pi R^3\sin^2\theta\cos\theta$$ $c=\cos^2\theta$ гэвэл $V(c)=4\pi R^3(1-c^2)c,\ 0\le c\le 1$ байна. $$V^\prime(c)=0\Rightarrow 1-3c^2=0\Rightarrow c=\dfrac{\sqrt3}{3}$$ үед ХИУ-тай. Энэ үед $\sin\theta=\sqrt{1-c^2}=\dfrac{\sqrt6}{3}$ байна. Суурийн периметр нь $2\pi r=2\pi R\sin\theta$ тул хажуу гадаргуугийн талбай нь $$S_{\text{хг}}=4\pi R^2\sin\theta\cos\theta=4\pi R^2\cdot\dfrac{\sqrt6}{3}\cdot\dfrac{\sqrt3}{3}=\dfrac{4\sqrt2\pi R^2}{3}$$ байна.
Эзлэхүүн нь $$V=S_{суурь}\cdot h=\pi r^2h=4\pi R^3\sin^2\theta\cos\theta$$ $c=\cos^2\theta$ гэвэл $V(c)=4\pi R^3(1-c^2)c,\ 0\le c\le 1$ байна. $$V^\prime(c)=0\Rightarrow 1-3c^2=0\Rightarrow c=\dfrac{\sqrt3}{3}$$ үед ХИУ-тай. Энэ үед $\sin\theta=\sqrt{1-c^2}=\dfrac{\sqrt6}{3}$ байна. Суурийн периметр нь $2\pi r=2\pi R\sin\theta$ тул хажуу гадаргуугийн талбай нь $$S_{\text{хг}}=4\pi R^2\sin\theta\cos\theta=4\pi R^2\cdot\dfrac{\sqrt6}{3}\cdot\dfrac{\sqrt3}{3}=\dfrac{4\sqrt2\pi R^2}{3}$$ байна.