Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
ЭЕШ 2017 B №21
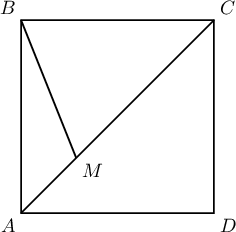
$ABCD$ квадратын $AC$ диагоналийг $M$ цэг $AM=5$, $MC=7$ байхаар хуваажээ. $BM$-ийн уртыг ол.
A.$6$ B.$5\sqrt2$ C.$4\sqrt3$ D.$\sqrt{37}$ E.$3\sqrt{3}$
Бодлогын төрөл:Сонгох
Амжилтын хувь:35.14%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:
$\angle BHM=90^\circ$ болохыг ашиглан бод.
$\angle BHM=90^\circ$ болохыг ашиглан бод.
Бодолт:Квадратын диагоналын урт нь $5+7=12$ байна. Диагоналын хагас нь $6$ тул $BH=6$, $MH=AH-AM=7-6=1$ байна. Иймд Пифагорын теоремоор
$$BM=\sqrt{1^2+6^2}=\sqrt{37}$$
байна.
Сорилго
ЭЕШ 2017 B ДӨРВӨН ӨНЦӨГТ ЭЕШ 2017 B ЭЕШ 2017 B тестийн хуулбар 2024-03-16 сургуулийн сорил 2024-03-16 сургуулийн сорил тестийн хуулбар 2024-05-30 2025-09-17 12в ангийн 2 дахь сорил