Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
ЭЕШ 2017 B №31
Нэгж тойрог дээр орших $A\left(\frac{\sqrt2}{2};\frac{\sqrt2}{2}\right)$; $B\left(-\frac{\sqrt2}{2};\frac{\sqrt2}{2}\right)$ цэгүүд өгөгдөв. Тойрог дээр санамсаргүй $C$ цэг авахад $ABC$ хурц өнцөгт гурвалжин болох магадлалыг ол.
A. $\dfrac16$
B. $\dfrac34$
C. $\dfrac12$
D. $\dfrac14$
E. $\dfrac18$
Бодлогын төрөл: Сонгох
Амжилтын хувь: 29.15%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $\triangle ABC$ хурц өнцөгт байх $C$ цэгийн геометр байрыг нэгж тойрог дээр заагаад геометр магадлалын томьёо ашиглан бод.
Бодолт: $A\left(\frac{\sqrt2}{2};\frac{\sqrt2}{2}\right)$; $B\left(-\frac{\sqrt2}{2};\frac{\sqrt2}{2}\right)$; $A'\left(-\frac{\sqrt2}{2};-\frac{\sqrt2}{2}\right)$; $B'\left(\frac{\sqrt2}{2};-\frac{\sqrt2}{2}\right)$ гэе.
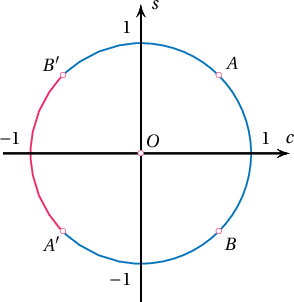$C$ цэг $AB'$ богино нум дээр байх үед $A$ өнцөг мохоо, $A'B$ богино нум дээр байх үед $B$ өнцөг мохоо, $AB$ богино нум дээр байх үед $C$ өнцөг мохоо байна. Харин $A'B'$ богино нум дээр байх үед бүх өнцөг нь хурц байна. Иймд $ABC$ гурвалжин хурц өнцөгт гурвалжин байх магадлал нь
$$\dfrac{\overset{\smile}{A'B'}}{2\pi}=\dfrac{\frac{\pi}{2}}{2\pi}=\dfrac14$$
байна.
Сорилго
ЭЕШ 2017 B
Магадлал, Статистик 2
Дундговь сорилго 3
Магадлал, Статистик 2 тестийн хуулбар
ЭЕШ 2017 B
ЭЕШ 2017 B тестийн хуулбар