Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Бодлого №13772
$ABC$ гурвалжинд $BD$ медиан татжээ. $AB=2\sqrt3$, $AC=8$, $\measuredangle ABD=45^\circ$ бол $BC$ талын уртыг ол.
A. $\sqrt6+\sqrt{10}$
B. $4\sqrt3$
C. $16+4\sqrt{15}$
D. $\sqrt{52+8\sqrt{15}}$
E. $2\sqrt{100-2\sqrt{15}}$
Бодлогын төрөл: Сонгох
Амжилтын хувь: 15.79%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Гурвалжны медиан:
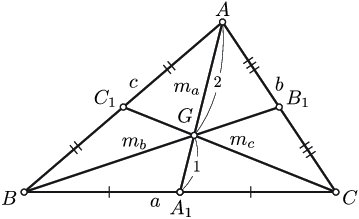Гурвалжны гурван медиан нэг цэгт огтлолцоно. Энэ цэг нь гурвалжны хүндийн төв болох бөгөөд $$AG:GA_1=BG:GB_1=CG:GC_1=2:1$$ байна. Медианы урт нь:
$$m_a^2=\dfrac{2(b^2+c^2)-a^2}{4},\quad m_b^2=\dfrac{2(a^2+c^2)-b^2}{4},\quad m_c^2=\dfrac{2(a^2+b^2)-c^2}{4}.$$
Бодолт: $AD=AC/2=4$. Косинусын теоремоор $$AD^2=AB^2+BD^2-2\cdot AB\cdot BD\cdot\cos 45^\circ\Rightarrow$$ $$4^2=(2\sqrt3)^2+BD^2-2\cdot 2\sqrt3\cdot BD\cdot\frac{\sqrt2}{2}\Rightarrow BD^2-2\sqrt6 BD-4=0.$$ Эндээс $BD=\dfrac{2\sqrt6\pm\sqrt{(2\sqrt6)^2-4\cdot(-4)}}{2}=\sqrt6\pm\sqrt10$. $BD>0$ тул $BD=\sqrt6+\sqrt{10}$. $m_b^2=\dfrac{2(a^2+c^2)-b^2}{4}$ тул $$a^2=\dfrac{4m_b^2+b^2-2c^2}{2}=\dfrac{4(\sqrt6+\sqrt{10})^2+8^2-2(2\sqrt3)^2}{2}=52+8\sqrt{15}\Rightarrow$$ $BC=a=\sqrt{52+8\sqrt{15}}$.