Монгол Бодлогын Сан

Заавар: Косинусын теорем ашиглан $|AC|$, $|AD|$-г олоод $$S=\dfrac12ab\sin\gamma$$ гурвалжны талбай олох томьёог ашигла.

Бодолт: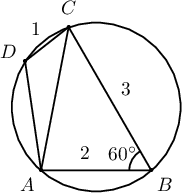

$ABC$ гурвалжинд косинусын теорем бичвэл $$AC^2=AB^2+BC^2-2AB\cdot BC\cdot\cos\angle B$$ буюу $$AC^2=2^2+3^2-2\cdot 2\cdot 3\cdot\dfrac12=7$$ $ABCD$ тойрогт багтсан тул $\angle B+\angle D=180^\circ$ буюу $\angle D=180^\circ-60^\circ=120^\circ$.

$ADC$ гурвалжинд косинусын теорем бичвэл $$AC^2=AD^2+DC^2-2AD\cdot DC\cdot\cos\angle D$$ буюу $$7=AD^2+1-2AD\cdot 1\cdot\cos 120^\circ\Leftrightarrow AD^2+AD-6=0$$ Квадрат тэгшитгэлийг бодвол $AD=-3$, $AD=2$ шийд гарах боловч $AD>0$ тул $AD=2$. Иймд \begin{align*} S_{ABCD}&=S_{ABC}+S_{ADC}=\dfrac{1}{2}\cdot 2\cdot 3\cdot\sin 60^\circ+\dfrac12\cdot 1\cdot 2\cdot\sin120^\circ\\ &=\dfrac{1}{2}\cdot 2\cdot 3\cdot\dfrac{\sqrt3}{2}+\dfrac12\cdot 1\cdot 2\cdot\dfrac{\sqrt3}{2}=2\sqrt{3} \end{align*}