Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Бодлого №15419
Хайрцагт 12 улаан, 8 ногоон, 10 цэнхэр бөмбөг байв. 2 бөмбөг таамгаар авахад тэр нь цэнхэр биш гэдэг нь мэдэгдэж байсан бол:
- хоёул ногоон байх магадлал $\dfrac{\fbox{ab}}{\fbox{cd}}$
- улаан ба ногоон өнгөтэй байх магадлал $\dfrac{\fbox{ef}}{\fbox{cd}}$
abcd = 1495
ef = 48
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 3.54%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Модны схем ашиглан бод.
Бодолт: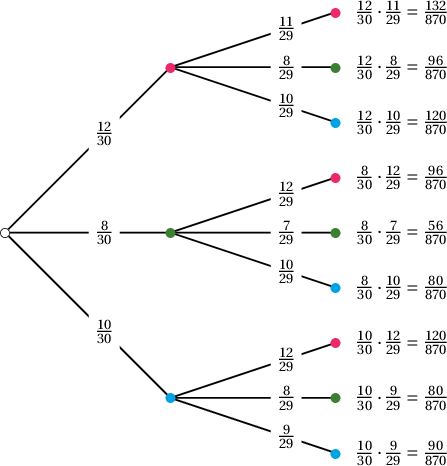 
Цэнхэр өнгө ороогүй байх магадлал
$$\dfrac{132}{870}+\dfrac{96}{970}+\dfrac{96}{970}+\dfrac{56}{970}=\dfrac{380}{970}$$
Эдгээрээс хоёул ногоон байх нь $\dfrac{56}{970}$ тул магадлал нь
$$\dfrac{56}{970}:\dfrac{380}{970}=\dfrac{56}{380}=\dfrac{14}{95}$$
улаан ба ногоон байх нь $\dfrac{96}{970}+\dfrac{96}{970}=\dfrac{192}{970}$ тул магадлал нь
$$\dfrac{192}{970}:\dfrac{380}{970}=\dfrac{192}{380}=\dfrac{48}{95}$$
байна.