Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Бодлого №15440
1 урттай хэрчим дээр 2 цэг хаяхад түүнийг 3 хэсэгт хуваав. Үүссэн хэрчмүүд гурвалжин үүсгэх магадлалыг ол.
A. $\dfrac12$
B. $\dfrac13$
C. $\dfrac23$
D. $\dfrac14$
E. $\dfrac34$
Бодлогын төрөл: Сонгох
Амжилтын хувь: 7.69%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $[0,1]$ хэрчим дээр хаясан цэгүүд нь $x$, $y$ координатуудтай байг. Хос тоо бүрийг хавтгай дээрх цэгийн координат гэж үзэж болно. $0\le x$, $y\le1$ тул $(x,y)$ цэг нь 1 талтай квадратад байрлана. Координатууд нь бодлогын нөхцөлийг хангах цэгүүд ямар дүрс үүсгэхийг ол.
Бодолт: $x\le y$ байх тохиолдолд хэрчмүүдийн урт $x$, $y-x$, $1-y$ байна. Гурвалжны тэнцэтгэл бишээр
$$\left\{\begin{array}{c}
x+(y-x)>1-y\\
x+(1-y)>y-x\\
(1-y)+(y-x)>x
\end{array}\right.\Leftrightarrow
\left\{\begin{array}{c}
0.5 < y\\
y< x+0.5\\
x < 0.5
\end{array}\right.\quad(1)$$
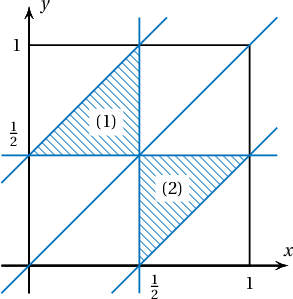$y\le x$ байх тохиолдолд хэрчмүүдийн урт $y$, $x-y$, $1-x$ байна. Гурвалжны тэнцэтгэл бишээр
$$\left\{\begin{array}{c}
y+(x-y)>1-x\\
y+(1-x)>x-y\\
(1-x)+(x-y)>x
\end{array}\right.\Leftrightarrow
\left\{\begin{array}{c}
0.5 < x\\
y< x-0.5\\
y < 0.5
\end{array}\right.\quad(2)$$