Монгол Бодлогын Сан

Заавар:

Бодолт: Хэрчмийн дээд үзүүрээс доод талдаа хамгийн ойр орших шулуун хүртэлх зайг $y$ гэе. Өгөгдсөн шулуунаас цагийн зүүний эсрэг тоолоход хэрчимтэй үүсгэх өнцгийг $x$ гэе. 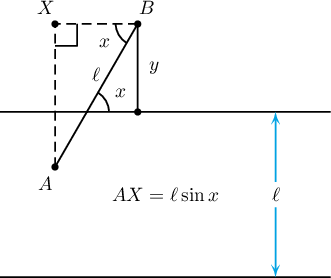Тэгвэл $0\le x\le\pi$, $0\le y\le\ell$ байх хос тоог олох ба $(x,y)$ цэгийг тэгш өнцөгтөд хаяжээ гэж үзэж болно. Хэрчим шулуунтай огтлолцохтой эн чацуу нөхцөл нь $y\le\ell\sin x$ юм. Энэ нь зураг дээрх зураасласан муж болох ба үүний талбай нь $$\sigma=\int^{\pi}_0\ell\sin x dx=2\ell$$ болно. Уг тэгш өнцөгтийн талбай $S=\pi\ell$ тул эрж буй магадлал нь $$p= \dfrac{\sigma}S= \dfrac{2\ell}{\pi\ell}= \dfrac2{\pi}\approx0.6316$$ болно.