Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Бодлого №15446
Тойрогт санамсаргүйгээр гурвалжин багтааж зурж байна. Тэр нь хурц өнцөгт гурвалжин байх магадлалыг ол.
Бодлогын төрөл: Уламжлалт
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: α, β өнцгүүдийг дураар авбал α+β<π байна. α<π2, β<π2 ба γ=π−α−β<π2 мужуудыг αβ хавтгайд дүрсэлж геометр магадлал бод.
Бодолт: αβ хавтгайд α, β, γ өнцгүүд бүхий гурвалжин хурц өнцөгт байх муж буюу α<π2, β<π2, π2<α+β тэнцэтгэл бишийн шийдийн муж нь нийт боломжит утгын 14 хэсэг болох нь харагдаж байна.
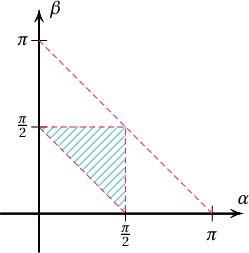Иймд дурын сонгож авсан гурвалжин хурц өнцөгт гурвалжин байх магадлал нь 14 ажээ.